题目内容
14.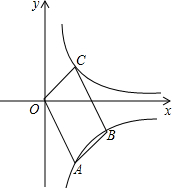 如图所示,四边形OABC为平行四边形,点A、B在反比例函数y=$\frac{{k}_{1}}{x}$图象上,点A(2,-4),边BC与x轴交于点D且D为BC中点,点C在反比例函数y=$\frac{{k}_{2}}{x}$图象上,则k2的值为( )
如图所示,四边形OABC为平行四边形,点A、B在反比例函数y=$\frac{{k}_{1}}{x}$图象上,点A(2,-4),边BC与x轴交于点D且D为BC中点,点C在反比例函数y=$\frac{{k}_{2}}{x}$图象上,则k2的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 先求得k1的值,作AE⊥x轴于E,BF⊥x轴于F,CG⊥x轴于G,证得△OAE∽△BDF,证得B的坐标,然后证得△CGD≌△BFD,即可求得C的坐标,从而求得k2的值.
解答 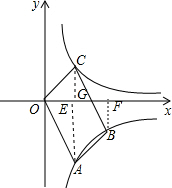 解:∵点A(2,-4)在反比例函数y=$\frac{{k}_{1}}{x}$图象上,
解:∵点A(2,-4)在反比例函数y=$\frac{{k}_{1}}{x}$图象上,
∴k1=2×(-4)=-8,
作AE⊥x轴于E,BF⊥x轴于F,CG⊥x轴于G,
∵四边形OABC是平行四边形,
∴OA∥BC,OA=BC,
∴∠AOB=∠BDF,
∵∠AEO=∠BFO=90°,
∴△OAE∽△BDF,
∴$\frac{BF}{AE}$=$\frac{DF}{OE}$=$\frac{BD}{OA}$,
∵BD=$\frac{1}{2}$BC,
∴$\frac{BF}{4}$=$\frac{DF}{2}$=$\frac{1}{2}$,
∴BF=2,DF=1,
把y=-2代入反比例函数y=-$\frac{8}{x}$得x=4,
∴B(4,-2),
在△CGD和△BFD中,
$\left\{\begin{array}{l}{∠CDG=∠BDF}\\{∠CGD=∠BFD=90°}\\{CD=BC}\end{array}\right.$,
∴△CGD≌△BFD(AAS),
∴CG=BF=2,GD=DF=1,
∴C(2,2),
∵点C在反比例函数y=$\frac{{k}_{2}}{x}$图象上,
∴k2=2×2=4,
故选B.
点评 本题考查了反比例函数图象上点的坐标特征,找出辅助线构建相似三角形和全等三角形是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
4.若线段AB=2,且点C是AB的黄金分割点,则BC等于( )
| A. | $\sqrt{5}-1$ | B. | 3-$\sqrt{5}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{5}-1$或3-$\sqrt{5}$ |
5.下列函数中,y是x的正比例函数是( )
| A. | y=-2x | B. | y=$\frac{2}{x}$ | C. | y=2x2 | D. | y=-2x+1 |
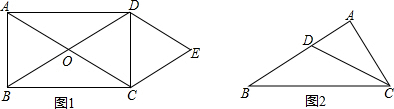
 如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).
如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).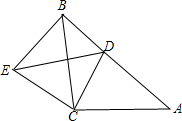 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.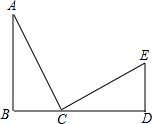 如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE.
如图,已知:AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,证明:AC⊥CE. 如图,点E为DF上一点,点B为AC上一点,且DB∥EC,∠C=∠D,∠A=40°,求∠F的度数.
如图,点E为DF上一点,点B为AC上一点,且DB∥EC,∠C=∠D,∠A=40°,求∠F的度数.