Question

已知⊙O半径为1，P为⊙O外一点，PA切⊙O于点A，PA=1，AB是⊙O的弦，且AB=，则PB²的值为________．

Answer 1

或
分析：先利用勾股定理逆定理求出∠PAB的度数，再利用余弦定理，分别讨论当点B位于左侧和右侧时的情况即可得出PB²的值．
解答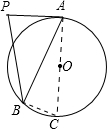：解：连接OA，并延长交⊙O与点C，连接BC
即有AB=，AC=2，
当点B在左侧时，
即可得出∠C=60°，
根据切线的性质定理，得∠BAP=60°，
在△APB中，
PA=1，AB=，∠PAB=60°，
根据余弦定理即有
PB²=4-；
同理当B在右侧是，PB²=4+．
点评：本题考查了能够切线的性质，并且要能够根据勾股定理的逆定理发现直角三角形，进一步利用余弦定理即可得出PB的平方．