题目内容
 如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1),△ABC的面积为
如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1),△ABC的面积为| 5 | 4 |
(1)求该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由.
分析:(1)由△ABC的面积为
,可得AB×OC=
,又二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1)可求得该二次函数的关系式;
(2)根据直线与圆的位置的位置关系确定m的取值范围.
(3)四边形ABCD为直角梯形,要分类讨论,即究竟那条边为底.可以分别以AC、BC为底进行讨论.
| 5 |
| 4 |
| 5 |
| 2 |
(2)根据直线与圆的位置的位置关系确定m的取值范围.
(3)四边形ABCD为直角梯形,要分类讨论,即究竟那条边为底.可以分别以AC、BC为底进行讨论.
解答:解:(1)∵OC=1,
∴q=-1,
∵△ABC的面积为
.
∴
OC×AB=
,
解得AB=
,
设A(a,0),B(b,0),
则a、b是一元二次方程x2+px-1=0两个根,
∴a+b=-p,ab=-1,
∴AB=b-a=
=
,
解得p=±
,
又∵p<0,
∴p=-
.
所以解析式为:y=x2-
x-1;
(2)令y=0,
解方程得x2-
x-1=0,
得x1=-
,x2=2,
所以A(-
,0),B(2,0),
在直角三角形AOC中可求得AC=
,同样可求得BC=
,
显然AC2+BC2=AB2,得三角形ABC是直角三角形.AB为斜边,
所以外接圆的直径为AB=
,
所以-
≤m≤
.

(3)存在,AC⊥BC,
①若以AC为底边,则BD∥AC,易求AC的解析式为y=-2x-1,
可设BD的解析式为y=-2x+b,
把B(2,0)代入得BD解析式为y=-2x+4,
解方程组
得D(-
,9)
②若以BC为底边,则BC∥AD,易求BC的解析式为y=0.5x-1,
可设AD的解析式为y=0.5x+b,把A(-
,0)代入
得AD解析式为y=0.5x+0.25,
解方程组
得D(
,
)
综上,所以存在两点:(-
,9)或(
,
).
∴q=-1,
∵△ABC的面积为
| 5 |
| 4 |
∴
| 1 |
| 2 |
| 5 |
| 4 |
解得AB=
| 5 |
| 2 |
设A(a,0),B(b,0),
则a、b是一元二次方程x2+px-1=0两个根,
∴a+b=-p,ab=-1,
∴AB=b-a=
| (a+b)2-4ab |
| 5 |
| 2 |
解得p=±
| 3 |
| 2 |
又∵p<0,
∴p=-
| 3 |
| 2 |
所以解析式为:y=x2-
| 3 |
| 2 |
(2)令y=0,
解方程得x2-
| 3 |
| 2 |
得x1=-
| 1 |
| 2 |
所以A(-
| 1 |
| 2 |
在直角三角形AOC中可求得AC=
| ||
| 2 |
| 5 |
显然AC2+BC2=AB2,得三角形ABC是直角三角形.AB为斜边,
所以外接圆的直径为AB=
| 5 |
| 2 |
所以-
| 5 |
| 4 |
| 5 |
| 4 |

(3)存在,AC⊥BC,
①若以AC为底边,则BD∥AC,易求AC的解析式为y=-2x-1,
可设BD的解析式为y=-2x+b,
把B(2,0)代入得BD解析式为y=-2x+4,
解方程组
|
得D(-
| 5 |
| 2 |
②若以BC为底边,则BC∥AD,易求BC的解析式为y=0.5x-1,
可设AD的解析式为y=0.5x+b,把A(-
| 1 |
| 2 |
得AD解析式为y=0.5x+0.25,
解方程组
|
得D(
| 5 |
| 2 |
| 3 |
| 2 |
综上,所以存在两点:(-
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题综合考查了二次函数的有关知识以及直线与圆的关系,范围较广,难度较大.

练习册系列答案
相关题目
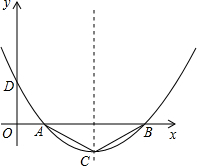 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b