题目内容
17.如图,AB∥CD,P1、P2、P3是AB与CD之间的点,且它们与A、B可组成一个凸多边形的顶点.(1)在图(1)中,求∠A+∠P1+∠C的度数;
(2)在图(2)中,求∠A+∠P1+∠P2+∠C的度数;
(3)直接写出图(3)中,∠A+∠P1+∠P2+∠P3+∠C的度数;如果在AB与CD之间有如图所示的P1、P2、P3,…,Pn这样的n个点,试求∠A+∠P1+∠P2+∠P3+…+∠Pn+∠C的度数(结果用含n的式子表示).

分析 (1)连接AC,根据三角形的内角和定理可知∠CAP1+∠P1+∠P1CA=180°,再由AB∥CD可得出∠BAC+∠ACD=180°,把两式相加即可;
(2)连接AC,同(1)可得∠CAP1+∠P1+∠P2+∠P2CA=360°,再由∠BAC+∠ACD=180°可得出结论;
(3)根据(1)、(2)的结论可得出规律.
解答 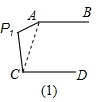 解:(1)如图1,连接AC,则∠CAP1+∠P1+∠P1CA=180°,
解:(1)如图1,连接AC,则∠CAP1+∠P1+∠P1CA=180°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAP1+∠P1+∠P1CD=180°+180°=360°;
(2)如图2,连接AC,则∠CAP1+∠P1+∠P2+∠P2CA=360°.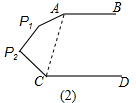
∵∠BAC+∠ACD=180°,
∴∠BAP1+∠P1+∠P2+∠P2CD=360°+180°=540°.
(3)如图3,连接AC,∠A+∠P1+∠P2+∠P3+∠C=720°.
当AB与CD之间有P1、P2、P3…Pn个这样的n个点时,连接AC,则多边形AP1P2P3…PnC是(n+2)边形,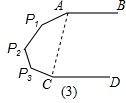
∴∠A+∠P1+∠P2+∠P3+…+∠P+∠C
=[(n+2)-2]×180°+180°=(n+1)×180°.
[另解]由以上可知,当AB与CD之间有1个点时,所求角的和为(1+1)×180°;
当AB与CD之间有2个点时,所求角的和为(2+1)×180°;
当AB与CD之间有3个点时,所求角的和为(3+1)×180°
当故AB与CD之间有n个点时,所求角的和为(n+1)×180°.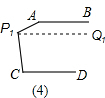 [解法二](1)如图(4),过点P1作P1Q1∥AB,则AB∥P1Q1∥CD,
[解法二](1)如图(4),过点P1作P1Q1∥AB,则AB∥P1Q1∥CD,
∴所求角的度数和=180°×2=360°;
(2)如图(5),分别过点P1P2作P1Q1∥AB,P2Q2∥AB,则AB∥P1Q1∥P2Q2∥CD,
∴所求角的度数和=180°×3=540°;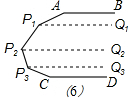
(3)同法可得,所求角的度数和=180°×4=720°,
由此类推,当AB与CD之间有P1、P2、P3…Pn这样的n个点时,分别过这n个点作AB的平行线,可得到(n+1)对互补的同旁内角.
∴这时所求角的度数和=(n+1)×180°.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. |  | B. |  | C. |  | D. |  |
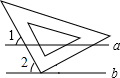 如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )
如图,直线a∥b,三角板的直角顶点放在直线b上,两直角边与直线a相交,如果∠1=55°,那么∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{12}-\sqrt{3}=3$ | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{12}÷\sqrt{3}=2$ |
 如图,已知线段AB=6延长线段AB到C,使BC=2AB,点D是AC的中点,则BD=3.
如图,已知线段AB=6延长线段AB到C,使BC=2AB,点D是AC的中点,则BD=3.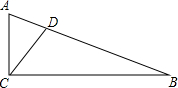 如图,CD为△ABC的角平分线,CD=2$\sqrt{2}$,若∠ACB=90°,△ABC的面积为10,则AB的长为2$\sqrt{15}$.
如图,CD为△ABC的角平分线,CD=2$\sqrt{2}$,若∠ACB=90°,△ABC的面积为10,则AB的长为2$\sqrt{15}$.