题目内容
如图，半圆的直径AB=12，P为AB上一点，点C，D为半圆的三等分点，求其中阴影部分的面积．
【答案】分析：连接OC、OD，利用同底等高的三角形面积相等可知阴影部分的面积等于扇形OCD的面积，然后计算扇形面积就可．
解答：解：连接OC、OD、CD．
∵△COD和△CPD等底等高，
∴S△COD=S△POD．
∵点C，D为半圆的三等分点，
∴∠COD=180°÷3=60°，
∴阴影部分的面积=S扇形COD=
=6π．
点评：本题的关键是理解阴影部分的面积等于扇形OCD的面积．
解答：解：连接OC、OD、CD．
∵△COD和△CPD等底等高，
∴S△COD=S△POD．
∵点C，D为半圆的三等分点，
∴∠COD=180°÷3=60°，
∴阴影部分的面积=S扇形COD=
=6π．点评：本题的关键是理解阴影部分的面积等于扇形OCD的面积．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
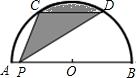如图，半圆的直径AB=10，P为AB上一点，点C，D为半圆的三等分点，则阴影部分的面积等于
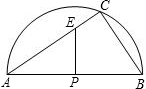如图，半圆的直径AB=10，P为圆心，点C在半圆上，BC=6．
（1997•新疆）如图，半圆的直径AB=3，点C在半圆上，点E在AC上，且AE=BC，EF⊥AB于点F．若设BC=x，EF=y，则y关于x的函数关系式为y=
如图，半圆的直径AB=10，点C在半圆上，BC=6．
如图，半圆的直径AB=10．弦AC=6，把AC沿直线AD对折恰与AB重合，点C落在C′处，则AD的长为（ ）