题目内容
1.(1)解分式方程:$\frac{3-x}{x-4}-\frac{2}{4-x}$=1.(2)先化简,再求值:($\frac{a^2}{{{a^2}-4a+4}}-\frac{a+2}{a-2}$)÷$\frac{4}{a-2}$,其中a=tan60°+4sin30°.
分析 (1)分式方程变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,利用特殊角的三角函数值求出a的值,代入计算即可求出值.
解答 解:(1)去分母得:x-3-2=4-x,
解得:x=$\frac{9}{2}$,
经检验x=$\frac{9}{2}$是分式方程的解;
(2)原式=[$\frac{{a}^{2}}{(a-2)^{2}}$-$\frac{(a+2)(a-2)}{(a-2)^{2}}$]•$\frac{a-2}{4}$=$\frac{4}{(a-2)^{2}}$•$\frac{a-2}{4}$=$\frac{1}{a-2}$,
当a=tan60°+4sin30°=$\sqrt{3}$+2时,原式=$\frac{\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.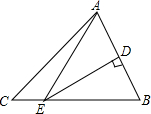 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
6.经过某十字路口的汽车,可能直行,也可能左转或者右转,如果这三种可能性大小相同,则经过这个十字路口的两辆汽车一辆左转,一辆右转的概率是( )
| A. | $\frac{4}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
13.计算3.8×107-3.7×107,结果用科学记数法表示为( )
| A. | 0.1×107 | B. | 0.1×106 | C. | 1×107 | D. | 1×106 |
7.在一次中学生田径运动会上,参加跳高的15名运动员的成绩如表:
那么这些运动员跳高成绩的中位数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 3 | 4 | 3 | 2 |
| A. | 4 | B. | 1.65 | C. | 1.70 | D. | 3 |
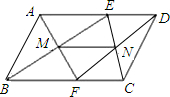 已知如图,在?ABCD中,E、F分别是AD、BC的中点,求证:MN∥BC,且MN=$\frac{1}{2}$BC.
已知如图,在?ABCD中,E、F分别是AD、BC的中点,求证:MN∥BC,且MN=$\frac{1}{2}$BC.