题目内容
如图，一个六边形的六个内角都是120°，连续四边的长依次是1、3、3、2．则该六边形的面积是分析：首先把这个六边形分割成两个等腰三角形，一个矩形和一个直角梯形，分别根据面积公式求出三角形、矩形和梯形的面积，这些图形的面积之和即为六边形的面积．
解答：
解：作图如下，
由题意知六边形的六个内角都是120°，
故知△ABC和△DEG均为等腰三角形，ACJF为矩形，FJDG为直角梯形，
△ABC的面积为
，四边形ACJF的面积为3
，梯形FJDG的面积为
，等腰梯形△DEG的面积为
，
故该六边形的面积是
+3
+
+
=
，
故答案为：
．
解：作图如下，由题意知六边形的六个内角都是120°，
故知△ABC和△DEG均为等腰三角形，ACJF为矩形，FJDG为直角梯形，
△ABC的面积为
9
| ||
| 4 |
| 3 |
5
| ||
| 2 |
| 3 |
故该六边形的面积是
9
| ||
| 4 |
| 3 |
5
| ||
| 2 |
| 3 |
| 35 |
| 4 |
| 3 |
故答案为：
| 35 |
| 4 |
| 3 |
点评：本题主要考查面积及等积变换的知识点，解答本题的关键是把这个六边形进行拆分，充分利用内角都为120°这一特点，本题难度不是很大．
练习册系列答案
备战中考寒假系列答案
相关题目
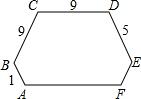如图所示，一个六边形的六个内角都是120°，其中连续四边的长依次是1、9、9、5．求这个六边形的周长．
如图，一个六边形的六个内角都是120°，连续四边的长依次是2.7，3，5，2，求该六边形周长．