题目内容
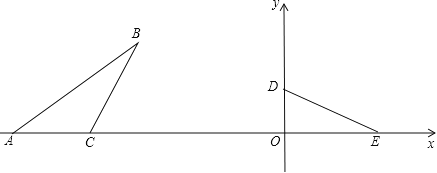
【题目】如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.
(1)求证:AB=CD;
(2)求证:CD2=BEBC;
(3)当CG= ![]() ,BE=
,BE= ![]() 时,求CD的长.
时,求CD的长.
【答案】
(1)证明:∵AC为⊙O的直径,
∴∠ABC=∠ADC=90°,
∵∠BAD=90°,
∴四边形ABCD是矩形,
∴AB=CD;
(2)∵AE为⊙O的切线,
∴AE⊥AC,
∴∠EAB+∠BAC=90°,
∵∠BAC+∠ACB=90°,
∴∠EAB=∠ACB,
∵∠ABC=90°,
∴△ABE∽△CBA,
∴ ![]() ,
,
∴AB2=BEBC,
由(1)知:AB=CD,
∴CD2=BEBC;
(3)∵F是AC的三等分点,
∴AF=2FC,
∵FG∥BE,
∴△AFG∽△ACB,
∴ ![]() =2,
=2,
设BG=x,则AG=2x,
∴AB=3x,
在Rt△BCG中,CG= ![]() ,
,
∴BC2=( ![]() )2﹣x2,
)2﹣x2,
BC= ![]() ,
,
由(2)得:AB2=BEBC,
(3x)2= ![]() ,
,
4x4+x2﹣3=0,
(x2+1)(4x2﹣3)=0,
x=± ![]() ,
,
∵x>0,
∴x= ![]() ,
,
∴CD=AB=3x= ![]() .
.
【解析】(1)要证AB=CD,由直径的性质和已知条件可证四边形ABCD是矩形,进而得出结论;(2)等积式CD2=BEBC由于无法构成三角形,因此须转化为AB2=BEBC,变形为![]() ,须证△ABE∽△CBA,由已知和直径的性质、切线的性质易证结论;(3)利用(2)的结论建立方程,AB2=BEBC
,须证△ABE∽△CBA,由已知和直径的性质、切线的性质易证结论;(3)利用(2)的结论建立方程,AB2=BEBC
由已知三等分点AF=2FC,可推出AG=2BG,设出BG=x,得方程(3x)2= ![]() ,由(1)得CD=AB=3x=
,由(1)得CD=AB=3x=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目