Question

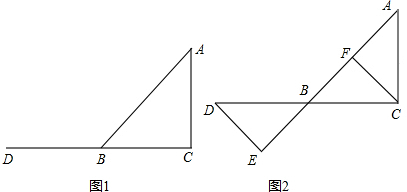
如图1，在△ABC，∠A=45°，延长CB至D，使得BD=BC．
（1）若∠ACB=90°，求证：BD=AC；
（2）如图2，分别过点D和点C作AB所在直线的垂线，垂足分别为E、F，求证：DE=CF．

Answer 1

解：（1）∵∠ACB=90°，∠A=45°，
∴△ABC为等腰直角三角形，
∴AC=BC，
而BC=BD，
∴BD=AC；
（2）∵CF⊥AB，DE⊥AB，
∴DE∥CF，
∴∠D=∠FCB，∠E=∠CFB，
在△BDE和△BCF中
，
∴△BDE≌△BCF（AAS），
∴DE=CF．
分析：（1）由∠ACB=90°，∠A=45°，可判断△ABC为等腰直角三角形，根据等腰直角三角形的性质得AC=BC，而BC=BD，则有BD=AC；
（2）根据在平面内垂直于同一直线的两直线平行得到DE∥CF，利用平行线的性质得∠D=∠FCB，∠E=∠CFB，然后根据三角形全等的判定方法可得到△BDE≌△BCF，则DE=CF．
点评：本题考查了全等三角形的判定与性质：有两组角分别相等，且其中一组角所对的边对应相等，那么这两个三角形全等；全等三角形的对应边相等．也考查了等腰直角三角形的判定与性质．