题目内容
如图所示．在梯形ABCD中，AB∥CD，AB＜CD．一条直线交BA延长线于E，交DC延长线于J，交AD于F，交BD于G，交AC于H，交BC于I．已知EF=FG=GH=HI=IJ，求DC：AB．
分析：由平行线可得对应线段成比例，又由已知EF=FG=CH=HI=IJ，可分别求出线段AB、CD与AE、CJ的关系，进而可求解结论．
解答：解：∵AB∥CD，EF=FG=CH=HI=IJ，
∴
=
=
，
∴
=
=
，
=
=
，
∴DJ=4AE，又
=
，
解得AB=
AE，
又AE=
CJ，
∴AB=
CJ，EB=4CJ，
=
=
，
CD=5CJ，
∴AB：CD=
：5=1：2．
∴
| BE |
| DJ |
| EG |
| GJ |
| 2 |
| 3 |
∴
| AE |
| CJ |
| EH |
| HJ |
| 3 |
| 2 |
| AE |
| DJ |
| EF |
| FJ |
| 1 |
| 4 |
∴DJ=4AE，又
| AB+AE |
| DJ |
| 2 |
| 3 |
解得AB=
| 5 |
| 3 |
又AE=
| 3 |
| 2 |
∴AB=
| 5 |
| 2 |
| EB |
| DJ |
| 4CJ |
| CD+CJ |
| 2 |
| 3 |
CD=5CJ，
∴AB：CD=
| 5 |
| 2 |
点评：本题主要考查了相似三角形对应边成比例或平行线分线段成比例的性质问题，应熟练掌握．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
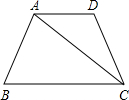已知如图所示，在梯形ABCD中，AD∥BC，AB=AD=DC=8，∠B=60°，连接AC．
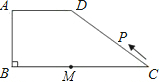如图所示，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，点M是线段BC上一定点，且MC=8．动点P从C点出发沿C?D?A?B的路线运动，运动到点B停止．在点P的运动过程中，使△PMC为等腰三角形的点P有
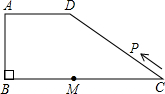如图所示，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，点M是线段BC上一定点，且MC=8．动点P从C点出发沿C→D→A→B的路线运动，运动到点B停止．在点P的运动过程中，使△PMC为等腰三角形的点P有几个？并求出相应等腰三角形的腰长．
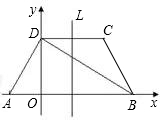如图所示，在梯形ABCD中，已知AB∥CD，AD⊥DB，AD=DC=CB，AB=4，DO垂直于AB．则腰长是
如图所示，在梯形ABCD中，AB∥DC，EF是梯形的中位线，AC交EF于G，BD交EF于H，以下说法错误的是（ ）