Question

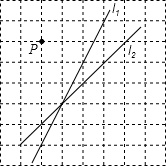如图，已知点P是半径为r的圆的圆心．
（1）当r=3时，请判断直线l₁与⊙P的位置关系，并写出理由．
（2）若直线l₂与⊙P相切，那么半径r为多少？写出具体过程．

Answer 1

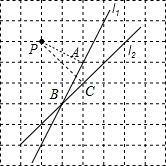解：（1）当r=3时，直线l₁与⊙P的位置关系是相交，
理由是：如图，连接PA，
则根据图形得出PA⊥l₁，
∵根据勾股定理得：PA==＜3，即d＜r，
∴当r=3时，直线l₁与⊙P的位置关系是相交；

（2）连接PC，
则根据图形得出PC⊥l₂，
∵根据勾股定理得：PC==2，
∵直线l₂与⊙P相切，
∴半径r=d=PC=2，
即半径r是2．
分析：（1）连接PA，根据图形得出得出PA⊥l₁，根据勾股定理得：PA=，得出d＜r，即可得出答案；
（2）连接PC，根据图形得出PC⊥l₂，根据勾股定理求出PC 根据直线与圆的位置关系得出即可．
点评：本题考查了勾股定理，直线与圆的位置关系，注意：当r=d时，直线与圆相切，当r＞d时，直线与圆相交，当r＜d时，直线与圆相离．