题目内容
20. 如图,某水渠的横断面是梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
如图,某水渠的横断面是梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.| A. | 1.2 | B. | 1.1 | C. | 0.8 | D. | 2.2 |
分析 过点E作EM⊥GH于点M,过点F作FN⊥GH于点N,可得四边形EFNM为矩形,可得MN=EF,然后设ME=FN=x,分别在Rt△GME和Rt△NHF中表示出GM和HN的长度,最后根据GH=6米,列出方程求出x的值.
解答 解: 过点E作EM⊥GH于点M,过点F作FN⊥GH于点N,
过点E作EM⊥GH于点M,过点F作FN⊥GH于点N,
可得四边形EFNM为矩形,
则MN=EF,
设ME=FN=x,
在Rt△GME中,
∵斜坡AD的坡度为1:1.2,
∴ME:GM=1:1.2,
∴GM=1.2x,
在Rt△NHF中,
∵斜坡BC的坡度为1:0.8,
∴NF:NH=1:0.8,
∴NH=0.8x,
则GH=1.2x+0.8x+3.8=6,
解得:x=1.1.
故选B.
点评 此题考查了解直角三角形的应用,用到的知识点是坡度、矩形的性质,关键是根据题意画出图形,作出辅助线,构造直角三角形.

练习册系列答案
相关题目
12.如图所示图形是轴对称图形的有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,△ABC中,AB=AC,∠B=70°.
如图,△ABC中,AB=AC,∠B=70°.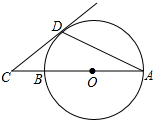 如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=
如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD= 一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.
一个几何体,是由许多规格相同的小正方体堆积而成的,从正面看和从左面看的形状如图所示,要搭成这样的几何体,最少需用6块小正方体.