题目内容
 边长为4的正方形置于平面直角坐标系中,使AB边落在x轴的正半轴上,且A点的坐标是(1,0).
边长为4的正方形置于平面直角坐标系中,使AB边落在x轴的正半轴上,且A点的坐标是(1,0).①直线y=
| 4 |
| 3 |
| 8 |
| 3 |
②若直线l1经过点F(-
| 3 |
| 2 |
分析:(1)由直线y=
x-
与x轴交与点E,即可求得点E的坐标,又由A点的坐标是(1,0),即可求得AE的长,又由CD=AD=4,即可求得四边形AECD的面积;
(2)由直线l1经过点F(-
,0)且与直线y=3x平行,可设直线l1的解析式为y=3x+b,然后由待定系数法即可求得直线l1;又由直线l:y=2x-3交x轴于点M,交直线l1于点N,即可求得M与N的坐标,继而求得△NMF的面积.
| 4 |
| 3 |
| 8 |
| 3 |
(2)由直线l1经过点F(-
| 3 |
| 2 |
解答:解:(1)∵直线y=
x-
与x轴交与点E,
当y=0时,即
x-
=0,
解得:x=2,
∴E(2,0),
∴OE=2.
∵A点的坐标是(1,0),
∴OA=1,
∴AE=OE-OA=1,
∵CD=AD=4,
∴S四边形ABCD=
(AE+CD)•AD=
×(1+4)×4=10;
若直线l1经过点F(-
,0)且与直线y=3x平行,直线l:y=2x-3交x轴于点M,交直线l1于点N,求△NMF的面积.
(2)∵直线l1与y=3x平行,
∴设直线l1:y=3x+b,
∵l1过点F(-
,0),
∴0=-
+b,
解得:b=
,
∴直线l1:y=3x+
;
直线l:y=2x-3,
y=0时,x=
,
∴M(
,0),
又∵
,
解得:
,
∴N(-
,-18),
∵MF=
+
=3,
∴S△NMF=
×3×18=27.
| 4 |
| 3 |
| 8 |
| 3 |
当y=0时,即
| 4 |
| 3 |
| 8 |
| 3 |
解得:x=2,
∴E(2,0),
∴OE=2.
∵A点的坐标是(1,0),
∴OA=1,
∴AE=OE-OA=1,
∵CD=AD=4,
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
若直线l1经过点F(-
| 3 |
| 2 |
(2)∵直线l1与y=3x平行,
∴设直线l1:y=3x+b,
∵l1过点F(-
| 3 |
| 2 |
∴0=-
| 9 |
| 2 |
解得:b=
| 9 |
| 2 |
∴直线l1:y=3x+
| 9 |
| 2 |
直线l:y=2x-3,

y=0时,x=
| 3 |
| 2 |
∴M(
| 3 |
| 2 |
又∵
|
解得:
|
∴N(-
| 15 |
| 2 |
∵MF=
| 3 |
| 2 |
| 3 |
| 2 |
∴S△NMF=
| 1 |
| 2 |
点评:此题考查了待定系数法求一次函数的解析式、点与一次函数的关系、正方形的性质、梯形的性质以及三角形的面积.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
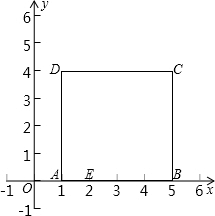 的坐标是(1,0).
的坐标是(1,0). 如图,边长为4的正方形置于直角坐标系中,如果A点的坐标为(3,2),则B点的坐标为
如图,边长为4的正方形置于直角坐标系中,如果A点的坐标为(3,2),则B点的坐标为 如图,将边长为4的正方形置于平面直角坐标系中,OE=3,点P为对角线DB上一动点,则PE+PA的最小值为
如图,将边长为4的正方形置于平面直角坐标系中,OE=3,点P为对角线DB上一动点,则PE+PA的最小值为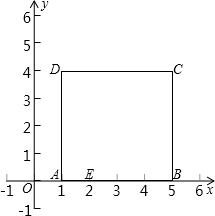 的坐标是(1,0).
的坐标是(1,0).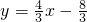 经过点C,且与x轴交于点E,求四边形AECD的面积;
经过点C,且与x轴交于点E,求四边形AECD的面积;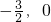 )且与直线y=3x平行.将(2)中直线l沿着y轴向上平移1个单位,交x轴于点M,交直线l1于点N,求△NMF的面积.
)且与直线y=3x平行.将(2)中直线l沿着y轴向上平移1个单位,交x轴于点M,交直线l1于点N,求△NMF的面积.