题目内容
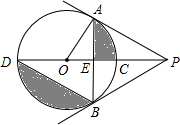 如图,直线PCD过圆心O,PA、PB分别切⊙O于A、B,∠APB=60°,PA=4,AB与PD相交于E.
如图,直线PCD过圆心O,PA、PB分别切⊙O于A、B,∠APB=60°,PA=4,AB与PD相交于E.(1)求弦AB的长;
(2)求阴影部分的面积.
分析:(1)根据切线长定理可以得出∠APB=60°,△PAB为等边三角形,即可求出;
(2)由S阴影=S半圆O-S△ADE,分别求出各部分的面积即可得出答案.
(2)由S阴影=S半圆O-S△ADE,分别求出各部分的面积即可得出答案.
解答: 解:(1)∵PA.PB与⊙O相切于A,B两点
解:(1)∵PA.PB与⊙O相切于A,B两点
∴PA=PB,
∵∠APB=60°,
∴△PAB为等边三角形,
∴AB=PA=4;
(2)连接AD,
∵PA,PB为⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴OP平分∠APB,OP垂直平分AB,
∴∠APO=
∠APB=30°,
∴∠AOP=60°,
∵∠PAO=90°,
∴OA=
=
=
,
∵AE=
AP=2,
∴AD=
AE=2
,
∴S阴影=S半圆O-S△ADE
=
π×(
)2-
×2×2
,
=
π-2
.
 解:(1)∵PA.PB与⊙O相切于A,B两点
解:(1)∵PA.PB与⊙O相切于A,B两点∴PA=PB,
∵∠APB=60°,
∴△PAB为等边三角形,
∴AB=PA=4;
(2)连接AD,
∵PA,PB为⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴OP平分∠APB,OP垂直平分AB,
∴∠APO=
| 1 |
| 2 |
∴∠AOP=60°,
∵∠PAO=90°,
∴OA=
| AP | ||
|
| 4 | ||
|
4
| ||
| 3 |
∵AE=
| 1 |
| 2 |
∴AD=
| 3 |
| 3 |
∴S阴影=S半圆O-S△ADE
=
| 1 |
| 2 |
4
| ||
| 3 |
| 1 |
| 2 |
| 3 |
=
| 8 |
| 3 |
| 3 |
点评:此题主要考查了切线长定理与扇形的面积公式等知识,求阴影部分面积不容易求出时,由特殊面积的差得出是常用方法.

练习册系列答案
相关题目
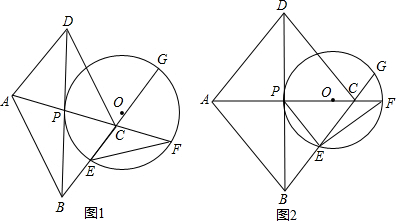 圆O与直线AC,BC分别交于点F,G.
圆O与直线AC,BC分别交于点F,G.