题目内容
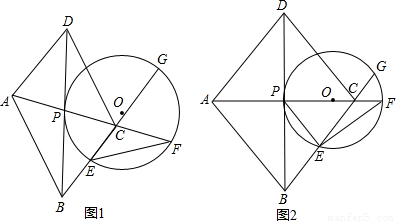
如图1,平行四边形ABCD的对角线AC,BD交于点P,E为BC的中点,过E点的圆O与BD相切于点P,圆O与直线AC,BC分别交于点F,G.(1)求证:△PCD∽△EPF;
(2)如果AB=AD,AC=6,BD=8(如图2).求圆O的直径.
【答案】分析:(1)由弦切角定理得,∠DPC=∠PEF,由平行四边形的性质和点E是BC的中点得PE∥CD,已知了∠CPE=∠PCD,可证得△PCD∽△EPF.
(2)由AB=AD,可证得平行四边形ABCD是菱形,则它的对角线互相垂直平分;根据勾股定理可求出菱形的边长.由于E是BC中点,可求得BE、EC的长,再根据切割线定理,可求出BG的长,进而可求出CG的长.在⊙O中,根据相交弦定理,可得PC•CF=EC•CG,其中PC、EC、CG的长已求得,由此可求出CF的长.也就求出了PF即圆的直径.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴BP=DP,
又∵BE=CE,
∴PE∥DC,
∴∠CPE=∠PCD,
∵BD切⊙O于P,
∴∠DPC=∠PEF,
∴△PCD∽△EPF;
(2)解:∵平行四边形ABCD中,AB=AD,
∴平行四边形ABCD为菱形.
∴AC⊥BD,PB= ,
,
BD= ×8=4,PC=
×8=4,PC= ,
,
AC= ×6=3,
×6=3,
∴BC=5,
∴BE=CE= ,
,
∵⊙O切BD于P,AC⊥BD,
∴PF为⊙O的直径,
∵PE2=BE•BG,
∴ ,
,
∴ ,
,
∴OG=BG-BC= ,
,
∵PC•CF=EC•CG,
∴ ,
,
∴ ,
,
∴⊙O的直径为 .
.
点评:本题综合利用了平行四边形的判定和性质,菱形的判定和性质,切割线定理,圆周角定理,相交弦定理求解.
(2)由AB=AD,可证得平行四边形ABCD是菱形,则它的对角线互相垂直平分;根据勾股定理可求出菱形的边长.由于E是BC中点,可求得BE、EC的长,再根据切割线定理,可求出BG的长,进而可求出CG的长.在⊙O中,根据相交弦定理,可得PC•CF=EC•CG,其中PC、EC、CG的长已求得,由此可求出CF的长.也就求出了PF即圆的直径.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴BP=DP,
又∵BE=CE,
∴PE∥DC,
∴∠CPE=∠PCD,
∵BD切⊙O于P,
∴∠DPC=∠PEF,
∴△PCD∽△EPF;
(2)解:∵平行四边形ABCD中,AB=AD,
∴平行四边形ABCD为菱形.
∴AC⊥BD,PB=
 ,
,BD=
 ×8=4,PC=
×8=4,PC= ,
,AC=
 ×6=3,
×6=3,∴BC=5,
∴BE=CE=
 ,
,∵⊙O切BD于P,AC⊥BD,
∴PF为⊙O的直径,
∵PE2=BE•BG,
∴
 ,
,∴
 ,
,∴OG=BG-BC=
 ,
,∵PC•CF=EC•CG,
∴
 ,
,∴
 ,
,∴⊙O的直径为
 .
.点评:本题综合利用了平行四边形的判定和性质,菱形的判定和性质,切割线定理,圆周角定理,相交弦定理求解.

练习册系列答案
相关题目
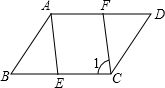 如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=( )
如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=( )| A、40° | B、50° | C、60° | D、80° |
 25、如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
25、如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE. 4、如图,在平行四边形ABCD中,BC=7cm,CD=5cm,∠D=50°,BE平分∠ABC,下列结论错误的是( )
4、如图,在平行四边形ABCD中,BC=7cm,CD=5cm,∠D=50°,BE平分∠ABC,下列结论错误的是( ) 19、如图,在平行四边形BCDE中,F为DE的中点,A为BE与CF延长线的交点,求证:CD=AE.
19、如图,在平行四边形BCDE中,F为DE的中点,A为BE与CF延长线的交点,求证:CD=AE.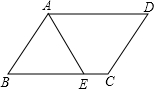 如图,在平行四边形ABCD中,AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则梯形AECD中位线的长等于
如图,在平行四边形ABCD中,AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则梯形AECD中位线的长等于