题目内容
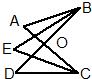如图，AC、BD相交于O，BE、CE分别平分∠ABD、∠ACD，且交于E，若∠A=60°，∠D=40°，则∠E=50°
50°
．分析：设AC与BE交于点P，得到∠1=∠2，∠3=∠4，利用三角形的内角和定理得：∠A+∠1=∠E+∠3①，∠A+∠1+∠2=∠D+∠3+∠4，即∠A+2∠1=∠D+2∠3②，然后①×2-②得，∠A=2∠E-∠D，而∠A=60°，∠D=40°，即可求出∠E．
解答：解：设AC与BE交于点P，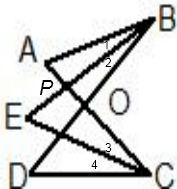
∵BE、CE分别平分∠ABD、∠ACD，
∴∠1=∠2，∠3=∠4，
在△APD和△EPC中，∠A+∠1=∠E+∠3①，
在△AOD和△DOC中，∠A+∠1+∠2=∠D+∠3+∠4，即∠A+2∠1=∠D+2∠3②，
①×2-②得，∠A=2∠E-∠D，
而∠A=60°，∠D=40°，
∴60°=2∠E-40°，
解得∠E=50°．
故答案为50°．
∵BE、CE分别平分∠ABD、∠ACD，
∴∠1=∠2，∠3=∠4，
在△APD和△EPC中，∠A+∠1=∠E+∠3①，
在△AOD和△DOC中，∠A+∠1+∠2=∠D+∠3+∠4，即∠A+2∠1=∠D+2∠3②，
①×2-②得，∠A=2∠E-∠D，
而∠A=60°，∠D=40°，
∴60°=2∠E-40°，
解得∠E=50°．
故答案为50°．
点评：本题考查了三角形的内角和定理：三角形的内角和为180°．
练习册系列答案
相关题目
8、如图，AC，BD相交于点O，AC=BD，AB=CD，写出图中两对相等的角
14、如图，AC和BD相交于点O，OA=OC，要使△AOB≌△COD还需添加一个条件是
22、如图，AC与BD相交于点P，若△ABC≌△DCB，则△ABP≌△DCP，理由是：
12、如图，AC与BD相交于点O，已知OA=OC，OB=OD，则△AOB≌△COD的理由是
如图，AC，BD相交于点O，且AB=DC，AC=DB．求证：∠ABO=∠DCO．