题目内容
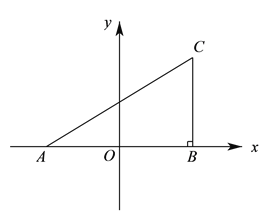
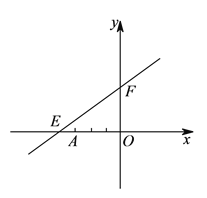
【题目】如图，直线
与
轴
轴分别交于点
、
，点的坐标为
，点
的坐标为
．
（
）求
的值．
（
）若点
是第二象限内的直线上的一个动点，在点
的运动过程中，试写出
的面积
与的函数关系式，并写出自变量的取值范围．
【答案】（
）
；（
）
（
）．
【解析】试题分析：
（1）把点E（-8，0）代入y=kx+6即可求得k的值；
（2）把（1）中所求得的k的值代入y=kx+6即可得到直线的解析式，由点P是直线第二象限内在直线y=kx+6上的点可得
结合OA=6即可得到S关于x的函数关系式，由点P在第二象限结合点E的坐标为（-8，0）即可得到x的取值范围为：-8<x<0.
试题解析：
（）∵
过
，
∴
，
．
（）∵，
∴
，
∵
在直线上，
∴
，
∴
，
∵在第二象限，且点E的坐标为（-8，0），
∴
．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
