��Ŀ����
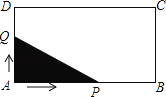
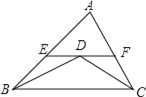
����Ŀ����ͼ1����DΪ��ABC��BC���ӳ�����һ�㣮

��1������A�á�ABC=3��4����ACD=140�㣬���A�Ķ�����
��2������ABC�Ľ�ƽ�������ACD�Ľ�ƽ���߽��ڵ�M������C��CP��BM�ڵ�P��
��֤�� ![]() ��
��
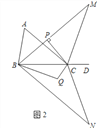
��3���ڣ�2���������£�����MBC��ֱ��BCΪ�Գ��ᷭ�۵õ���NBC����NBC�Ľ�ƽ�������NCB�Ľ�ƽ���߽��ڵ�Q����ͼ2������̽����BQC���A��������������ϵ����д����IJ��벢֤����
���𰸡���1��60��㣻
��2��֤����������
��3����BQC=90��+![]() ��A�����ɼ�����.
��A�����ɼ�����.
�������������������1���ȸ��ݡ�A����ABC=3��4�����A=3k����ABC=4k��������������ǵ��������k��ֵ�������ɵó����ۣ�
��2��������������ǵ����ʵó���M=��MCD-��MBC����A=��ACD-��ABC������MC��MB�ֱ�ƽ�֡�ACD����ABC�ó�![]() ,
, ![]() ,
,
��![]() ,����CP��BM���ɵó����ۣ�
,����CP��BM���ɵó����ۣ�
��3������BQƽ�֡�CBN��CQƽ�֡�BCN��֪![]() ,
, ![]() ���ٸ����������ڽǺͶ�����֪��
���ٸ����������ڽǺͶ�����֪�� ![]() ,������Գ�����֪��
,������Գ�����֪��
��M=��N���ɴ˿ɵó����ۣ�
��1���⣺��![]() �������
�������![]() ��
��
�֡�![]()
![]() �㣬
�㣬
��![]() �㣬
�㣬
��� ![]() �㣮
�㣮
��![]() �㣮
�㣮
��2��֤����
![]()
��3�������BQC=90��+![]() ��A��
��A��
֤�����£� ��BQƽ�֡�CBN��CQƽ�֡�BCN��
��![]() ��
��
��![]()
![]()
![]() ��
��
�ɣ�2��֪�� ![]() ��������Գ�����֪����M=��N��
��������Գ�����֪����M=��N��
��![]() ��
��
���⿼���������ε��ڽǺͣ���������ǵ����ʣ��۵�������.��1��������Σ�Ȼ�������ǵ�������⣻��2����Ͻ�ƽ���ߺ���ǵ�������⣻��2��������ԳƵ����ʺͣ�2���Ľ������.

 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д� Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�