Question

【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.

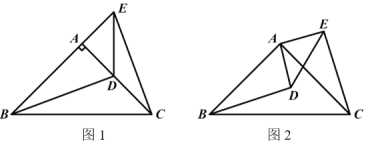
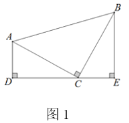
（1）当点D在AC上时,如下面图1,线段BD、CE有怎样的数量关系和位置关系？请直接写出结论，不需要证明.

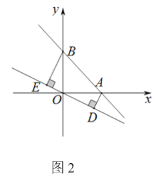
（2）将下面图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如下图2,上述关系是否成立？如果成立请说明理由.

Answer 1

【答案】（1）；（2）成立，见解析

【解析】

（1）根据SAS推知△ABD≌△ACE，然后由全等三角形的性质得出BD=CE，∠ABD=∠EAC，然后在△ABD和△CDF中，由三角形内角和定理可以求得∠CFD=90°，即BD⊥CE；

（2）根据SAS推知△ABD≌△ACE，然后由全等三角形的性质得出BD=CE，∠ABF=∠ECA，作辅助线BH构建对顶角，再根据三角形内角和即可得解.

（1）BD=CE，BD⊥CE；理由如下：

∵∠BAC=∠DAE=90°

∴∠BAD-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE

在△ABD与△ACE中，

∵AB=AC，∠BAD=∠CAE，AD=AE

∴△ABD≌△ACE（SAS）

∴BD=CE

延长BD交EC于F，如图所示：

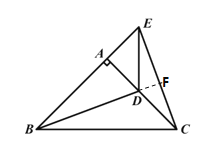
由△ABD≌△ACE，得∠ABD=∠EAC

∵∠ADB=∠CDF

∴∠CFD=∠DAB=90°

∴BD⊥CE；

（2）成立；理由如下：

延长BD交AC于F，交CE于H，如图所示：

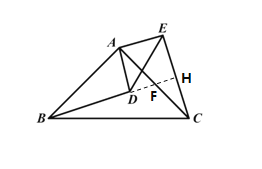
∵∠BAC=∠DAE=90°

∴∠BAD-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE

在△ABD与△ACE中，

∵AB=AC，∠BAD=∠CAE，AD=AE

∴△ABD≌△ACE（SAS）

∴BD=CE

在△ABF与△HCF中，

∵∠ABF=∠HCF，∠AFB=∠HFC

∴∠CHF=∠BAF=90°

∴BD⊥CE