题目内容
1.已知抛物线y=ax2+bx+c(a>0)与x轴分别交于(-1,0),(5,0)两点,当自变量x=1时,函数值为y1;当x=4时,函数值为y2.下列结论正确的是( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
分析 根据抛物线与x轴两交点分别是(-1,0),(5,0),先求对称轴,再借助对称轴以及函数的增减性求解即可.
解答 解:
∵抛物线y=ax2+bx+c(a>0)与x轴分别交于(-1,0),(5,0)两点,
∴抛物线的对称轴为直线x=$\frac{-1+5}{2}$=2,
∴自变量x=1时,函数值为y1和自变量x=3时,函数值y3相等,
∵a>0,
∴x>2时,y随x的增大而增大,
∵3<4,
∴y2>y3,
即y2>y1,
故选C.
点评 本题考查了抛物线和x轴交点的问题以及二次函数的增减性有关的性质,求出抛物线的对称轴是解题的关键.

练习册系列答案
相关题目
11. 某校男子篮球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的众数、中位数分别是( )
某校男子篮球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的众数、中位数分别是( )
 某校男子篮球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的众数、中位数分别是( )
某校男子篮球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的众数、中位数分别是( )| A. | 15,14.5 | B. | 14,15 | C. | 15,15.5 | D. | 15,15 |
12.《福布斯》中文版发布2015华人富豪榜,小米手机之父雷军依靠着132亿美元的身价成为湖北首富,132亿美元用科学记数法表示为( )美元.
| A. | 1.32×102 | B. | 13.2×109 | C. | 1.32×1010 | D. | 1.32×1011 |
9.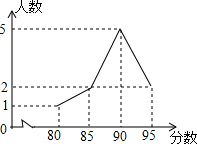 在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
 在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )| A. | 众数是90 | B. | 中位数是90 | C. | 平均数是89 | D. | 平均数是87.5 |
16.方程x2-4x-5=0的二次项系数和一次项系数分别为( )
| A. | 1和4 | B. | 1和-4 | C. | 1和-5 | D. | 1和5 |
13.在实数-4、2、0、-1中,最小数与最大数的积是( )
| A. | -2 | B. | 0 | C. | 4 | D. | -8 |
10.如图是一个几何体的三视图,则这个几何体是( )


| A. | 圆锥 | B. | 圆柱 | C. | 三棱锥 | D. | 长方体 |
11.将方程化为一元二次方程3x2-8x=10的一般形式,其中二次项系数,一次项系数,常数项分别是( )
| A. | 3,-8,-10 | B. | 3,-8,10 | C. | 3,8,-10 | D. | -3,-8,-10 |
 如图是用小正方体搭成的几何体的主视图和俯视图,俯视图上的数字表示小正方体的个数,则搭这个几何体最多要( )个小正方体.
如图是用小正方体搭成的几何体的主视图和俯视图,俯视图上的数字表示小正方体的个数,则搭这个几何体最多要( )个小正方体.