题目内容
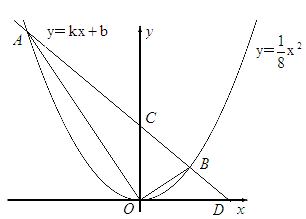
如图,直线 与抛物线
与抛物线 相交于A
相交于A ,B
,B 两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且
两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且 。
。
(1)求b的值;
(2)求证:点 在反比例函数
在反比例函数 的图象上;
的图象上;
(3)求证: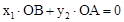 。
。
(1)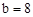
(2)把直线解析式化为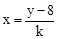 ,代入
,代入 得到关于y的一元二次方程
得到关于y的一元二次方程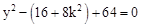 ,根据一元二次方程根与系数的关系,得到
,根据一元二次方程根与系数的关系,得到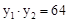 ,从而点
,从而点 在反比例函数
在反比例函数 的图象上。
的图象上。
(3)首先根据勾股定理和逆定理证明△OAB是直角三角形,从而得到△AEO∽△OFB,得比例式即可得证。
解析分析:(1)由直线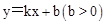 与x轴正半轴相交于点D,与y轴相交于点C,求出OC,OD,从而根据已知
与x轴正半轴相交于点D,与y轴相交于点C,求出OC,OD,从而根据已知 列式求解即可。
列式求解即可。
(2)把直线解析式化为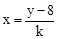 ,代入
,代入 得到关于y的一元二次方程
得到关于y的一元二次方程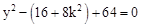 ,根据一元二次方程根与系数的关系,得到
,根据一元二次方程根与系数的关系,得到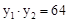 ,从而点
,从而点 在反比例函数
在反比例函数 的图象上。
的图象上。
(3)首先根据勾股定理和逆定理证明△OAB是直角三角形,从而得到△AEO∽△OFB,得比例式即可得证。
解:(1)∵直线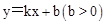 与x轴正半轴相交于点D,与y轴相交于点C,
与x轴正半轴相交于点D,与y轴相交于点C,
∴令x=0,得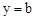 ;令y=0,得
;令y=0,得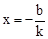 。∴OC=
。∴OC= ,OD=
,OD=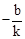 。
。
∴△OCD的面积 。
。
∵ ,∴
,∴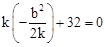 ,解得
,解得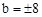 。
。
∵ 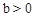 ,∴
,∴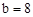 。
。
(2)证明:由(1),直线解析式为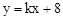 ,即
,即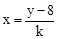 ,代入
,代入 ,得
,得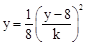 ,
,
整理,得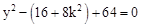 。
。
∵直线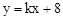 与抛物线
与抛物线 相交于A
相交于A ,B
,B ,
,
∴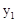 ,
,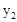 是方程
是方程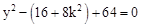 的两个根。
的两个根。
∴根据一元二次方程根与系数的关系,得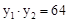 。
。
∴点 在反比例函数
在反比例函数 的图象上。
的图象上。
(3)证明:由勾股定理,得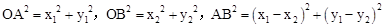 ,
,
由(2)得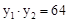 。
。
同理,将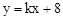 代入
代入 ,
,
得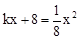 ,即
,即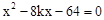 ,
,
∴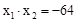 。
。
∴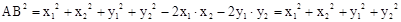 。
。
又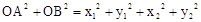 ,∴
,∴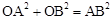 。
。
∴△OAB是直角三角形,即∠AOB=900。
如图,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,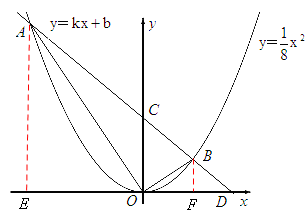
∵∠AOB=900,
∴∠AOE=900-∠BOF=∠OBF。
又∵∠AEO =∠OFB=900,
∴△AEO∽△OFB。∴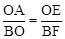 。
。
∵OE= ,BF=
,BF=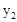 ,∴
,∴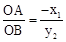 。
。
∴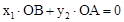 。
。

已知函数y= 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,Rt△ABC的顶点B在反比例函数y= 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是
| A.12 | B.4 | C.12- | D.12-3 |

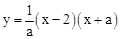 (a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.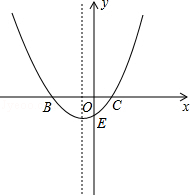
 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
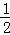 时,y的值.
时,y的值. 交y轴于点A,交x轴正半轴于点B.
交y轴于点A,交x轴正半轴于点B.
