Question

【题目】已知G是直角三角形ABC的内心，∠C=90°，AC=6，BC=8，则线段CG的长为______．

Answer 1

【答案】

【解析】试题分析： 作GD⊥AC于点D，作GE⊥BC于E，作GM⊥AB于M，连接GA、GB、GC，根据勾股定理求出AB，根据三角形的面积公式得出S△ACB=S△GAC+S△GBC+S△GAB，代入求出GE=2，由等腰直角三角形的性质和勾股定理即可得出CG的长．

解：作GD⊥AC于点D，作GE⊥BC于点E，作GM⊥AB于M，连接GA、GB、GC.如图所示：

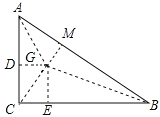
设GM=r，则GM=GD=GE=r，

∵AC=6,BC=8,∠C=90，

由勾股定理得：AB=10，

根据三角形的面积公式得：S△ACB=S△GAC+S△GBC+S△GAB，

∴AC×BC=AC×r+BC×r+AB×r，

即：×6×8=×6r+×8r+×10r，

解得：r=2.

则GE=2，

∵G是直角三角形ABC的内心，

∴∠GCE=∠C=45，

∴CG=GE=2

故答案为：.