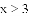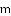��Ŀ����
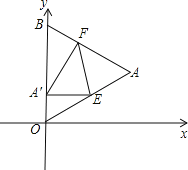
��ͼ����OAB�DZ߳�Ϊ2+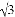 �ĵȱ������Σ�����O������ԭ�㣬����B��y���������ϣ�����OAB�۵���ʹ��A���ڱ�OB�ϣ���ΪA�䣬�ۺ�ΪEF��
�ĵȱ������Σ�����O������ԭ�㣬����B��y���������ϣ�����OAB�۵���ʹ��A���ڱ�OB�ϣ���ΪA�䣬�ۺ�ΪEF��
��1����A��E��x��ʱ�����A���E�����ꣻ
��2����A��E��x�ᣬ��������y=�� x2+bx+c������A���Eʱ������������x��Ľ�������ꣻ
x2+bx+c������A���Eʱ������������x��Ľ�������ꣻ
��3������A����OB���˶����������O��B�غ�ʱ���ܷ�ʹ��A��EF��Ϊֱ�������Σ����ܣ��������ʱ��A������ꣻ�����ܣ�����˵�����ɣ�
��ϰ��ϵ�д�
�����Ŀ
ij��˾��A��B���ֿͳ������ǵ��ؿ�����������±���������ѧ����ʵ��������ƻ���A��B�ͳ���5����ͬʱ�����꼶ʦ����У���زμ����ʵ�����
A | B | |
�ؿ�������/���� | 40 | 20 |
���Ԫ/���� | 200 | 150 |
��1����Ҫ��֤�����ò�����980Ԫ�����ʸ�ѧУ���ļ����������
��2���ڣ�1���������£������꼶ʦ������150�ˣ��������������ʡǮ��

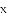
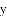
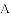
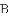
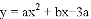 ������
������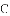
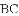
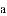
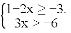 �Ľ⼯��__________.
�Ľ⼯��__________.
 D. 2
D. 2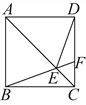
 �£�x��
�£�x�� ����
���� =3��
=3��
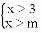 �Ľ⼯��
�Ľ⼯��