Question

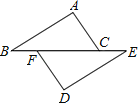
【题目】如图，△ABC是等边三角形，△ADC与△ABC关于直线AC对称，AE与CD垂直交BC的延长线于点E，∠EAF＝45°，且AF与AB在AE的两侧，EF⊥AF．

（1）依题意补全图形．

（2）①在AE上找一点P，使点P到点B，点C的距离和最短；

②求证：点D到AF，EF的距离相等．

Answer 1

【答案】（1）详见解析；（2）①详见解析；②详见解析．

【解析】

（1）本题考查理解题意能力，按照题目所述依次作图即可．

（2）①本题考查线段和最短问题，需要通过垂直平分线的性质将所求线段转化为其他等量线段之和，以达到求解目的．

②本题考查垂直平分线的判定以及全等三角形的证明，继而利用角的平分线性质即可得出结论．

（1）补全图形，如图1所示

（2）①如图2，连接BD，P为BD与AE的交点

∵等边△ACD，AE⊥CD

∴PC=PD,PC+PB最短等价于PB+PD最短

故B,D之间直线最短，点P即为所求．

②证明：连接DE，DF．如图3所示

∵△ABC，△ADC是等边三角形

∴AC＝AD，∠ACB＝∠CAD＝60°

∵AE⊥CD

∴∠CAE＝∠CAD＝30°

∴∠CEA＝∠ACB﹣∠CAE＝30°

∴∠CAE＝∠CEA

∴CA＝CE

∴CD垂直平分AE

∴DA＝DE

∴∠DAE＝∠DEA

∵EF⊥AF，∠EAF＝45°

∴∠FEA＝45°

∴∠FEA＝∠EAF

∴FA＝FE，∠FAD＝∠FED

∴△FAD≌△FED（SAS）

∴∠AFD＝∠EFD

∴点D到AF，EF的距离相等．