Question

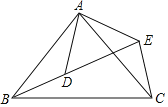
【题目】如图，AB＝AC，AD＝AE，点D在线段BE上，且∠BAC＝∠DAE．当∠BAD＝15°，∠ACE＝25°时，∠BEC＝_____．

Answer 1

【答案】100°．

【解析】

根据已知条件可证明△BAD≌△CAE,得出∠ABD＝25°，∠CAE＝15°,从而得出∠ADE＝∠ABD+∠BAD＝40°，∠AEC＝140°,又因为AD=AE,进一步得出结论.

解：∵∠BAC＝∠DAE，

∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，

∴∠BAD＝∠CAE，

在△BAD和△CAE中，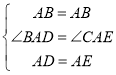

∴△BAD≌△CAE（SAS），

∴∠ABD＝∠ACE，

∵∠BAD＝15°，∠ACE＝25°，

∴∠ABD＝25°，∠CAE＝15°，

∴∠ADE＝∠ABD+∠BAD＝40°，∠AEC＝140°，

∵AD＝AE，

∴∠ADE＝∠AED，

∴∠AED＝40°，

∴∠BEC＝∠AEC﹣∠AED＝140°﹣40°＝100°，

故答案为：100°．