题目内容
一个直角三角形斜边上的两个三等分点与直角顶点的两条连线段长分别为3cm和4cm,则斜边长为________cm.
3
分析:过A作BD,BE的平行线,分别交CB延长线于G,H,由平行线的性质可得到AH,AG的长,假设BC=2k,则CG=3k,CH=6k,BG=k,BH=4k,由勾股定理可得到AH2-BH2=AG2-BG2=AB2,进而可求出k的值,再由勾股定理即可得到AC的长.
解答: 解:过A作BD,BE的平行线,分别交CB延长线于G,H,
解:过A作BD,BE的平行线,分别交CB延长线于G,H,
∴△CBD∽△CGA,
∴ =
= =
= ,
, =
= =
= ,
,
∴AH=12,AG=4.5,
假设BC=2k,则CG=3k,CH=6k,BG=k,BH=4k,
∵△ABG与△ABH有公共直角边AB,
∴AH2-BH2=AG2-BG2=AB2,
解得k= ,
,
∴BC2=(2k)2=33,AB2=AG2-BG2=12,
AC= =
=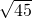 =3
=3 .
.
点评:本题考查的是相似三角形的判定与性质及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出相似三角形,再根据相似三角形的判定及性质解答.

分析:过A作BD,BE的平行线,分别交CB延长线于G,H,由平行线的性质可得到AH,AG的长,假设BC=2k,则CG=3k,CH=6k,BG=k,BH=4k,由勾股定理可得到AH2-BH2=AG2-BG2=AB2,进而可求出k的值,再由勾股定理即可得到AC的长.
解答:
 解:过A作BD,BE的平行线,分别交CB延长线于G,H,
解:过A作BD,BE的平行线,分别交CB延长线于G,H,∴△CBD∽△CGA,
∴
 =
= =
= ,
, =
= =
= ,
,∴AH=12,AG=4.5,
假设BC=2k,则CG=3k,CH=6k,BG=k,BH=4k,
∵△ABG与△ABH有公共直角边AB,
∴AH2-BH2=AG2-BG2=AB2,
解得k=
 ,
,∴BC2=(2k)2=33,AB2=AG2-BG2=12,
AC=
 =
=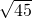 =3
=3 .
.点评:本题考查的是相似三角形的判定与性质及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出相似三角形,再根据相似三角形的判定及性质解答.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
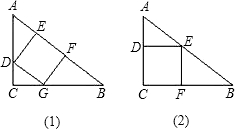 一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?
一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大? 一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?
一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?


