题目内容
已知:如图(1),∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.

(1)如图(2),若α=90゜,β=30゜,则∠MON=______.
(2)如图(3),若∠COD绕O逆时针旋转,且∠BOD=γ,求∠MON.
(3)如图(4),若α=2β,∠COD绕O逆时针旋转,转速为3゜/秒,∠AOB绕O同时逆时针旋转,转速为
1゜/秒,(转到OC与OA共线时停止运动),且OE平分∠BOD,以下两个结论:① 为定值;②∠AOD-∠COE为定值,请选择正确的结论,并说明理由.
为定值;②∠AOD-∠COE为定值,请选择正确的结论,并说明理由.
解:(1)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
α=90゜,β=30゜,
∴∠MON= α+
α+ β=60°;
β=60°;
故答案为:60゜;
(2)∵∠MOD=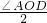 =
=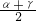 ,∠NOB=
,∠NOB= =
=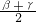 ,
,
∴∠MON=∠MOD+∠NOB-∠DOB=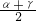 +
+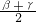 -γ=
-γ= ;
;
(3)① 为定值
为定值 ,
,
设运动时间为t秒,则∠DOB=3t-t=2t,∠DOE= ∠DOB=t,
∠DOB=t,
∴∠COE=β+t.∠AOD=α+2t,
又∵α=2β,
∴∠AOD=2β+2t=2(β+t).
∴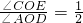 .
.
分析:(1)利用角平分线的性质即可得出∠MON= ∠AOD+
∠AOD+ ∠BOC,进而求出即可;
∠BOC,进而求出即可;
(2))利用∠MOD=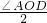 =
=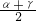 ,∠NOB=
,∠NOB= =
=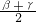 ,进而得出即可;
,进而得出即可;
(3)利用已知表示出∠COE和∠AOD,进而得出答案.
点评:此题主要考查了角的计算,正确根据角平分线的性质得出是解题关键.
α=90゜,β=30゜,
∴∠MON=
 α+
α+ β=60°;
β=60°;故答案为:60゜;
(2)∵∠MOD=
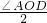 =
=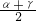 ,∠NOB=
,∠NOB= =
=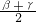 ,
,∴∠MON=∠MOD+∠NOB-∠DOB=
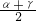 +
+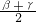 -γ=
-γ= ;
;(3)①
 为定值
为定值 ,
,设运动时间为t秒,则∠DOB=3t-t=2t,∠DOE=
 ∠DOB=t,
∠DOB=t,∴∠COE=β+t.∠AOD=α+2t,
又∵α=2β,
∴∠AOD=2β+2t=2(β+t).
∴
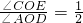 .
.分析:(1)利用角平分线的性质即可得出∠MON=
 ∠AOD+
∠AOD+ ∠BOC,进而求出即可;
∠BOC,进而求出即可;(2))利用∠MOD=
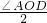 =
=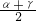 ,∠NOB=
,∠NOB= =
=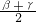 ,进而得出即可;
,进而得出即可;(3)利用已知表示出∠COE和∠AOD,进而得出答案.
点评:此题主要考查了角的计算,正确根据角平分线的性质得出是解题关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为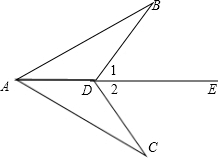 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为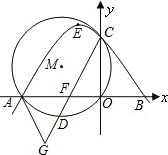 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧