题目内容
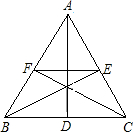如图，设AD、BE、CF为△ABC的三条高，若AB=6，BC=5，EF=3，则线段BE的长为分析：此题考查了直角三角形的性质和锐角三角函数的性质．
解答：解：∵AD，BE，CF为△ABC的三条高，易知B，C，E，F四点共圆，
∴△AEF∽△ABC，
∴
=
=
，
即cos∠BAC=
，
∴sin∠BAC=
，
∴在Rt△ABE中，BE=ABsin∠BAC=6 •
=
．
故答案为：
．
∴△AEF∽△ABC，
∴
| AF |
| AC |
| EF |
| BC |
| 3 |
| 5 |
即cos∠BAC=
| 3 |
| 5 |
∴sin∠BAC=
| 4 |
| 5 |
∴在Rt△ABE中，BE=ABsin∠BAC=6 •
| 4 |
| 5 |
| 24 |
| 5 |
故答案为：
| 24 |
| 5 |
点评：本题是一道根据直角三角形的性质结合角的三角函数求解的综合题，要注意圆的性质应用；要注意数形结合思想的应用．
练习册系列答案
相关题目
如图，设AD，BE，CF为三角形ABC的三条高，若AB=6，BC=5，EF=3，则线段BE的长为（ ）A、
| ||
| B、4 | ||
C、
| ||
D、
|
如图，设AD、BE、CF为三角形ABC的三条高，若AB=6，BC=5，AE-EC=
