题目内容
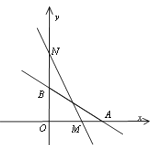
【题目】如图,直线L:![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,在y轴上有一点
两点,在y轴上有一点![]() ,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
(1)点A的坐标: ;点B的坐标: ;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() ,求出此时点M的坐标;
,求出此时点M的坐标;
【答案】(1)(8,0),(0,6);(2)①当点M在y轴右侧时,OM=OA-AM=8-t,![]() (0≤t<8);②当点M在y轴左侧时,OM=AM-OA=t-8;
(0≤t<8);②当点M在y轴左侧时,OM=AM-OA=t-8;![]() (t>8);(3)当t=5或11时,
(t>8);(3)当t=5或11时,![]() ,此时点M的坐标分别为(3,0),(-3,0).
,此时点M的坐标分别为(3,0),(-3,0).
【解析】
(1)在![]() 中,分别令y=0和x=0,则可求得A、B的坐标;
中,分别令y=0和x=0,则可求得A、B的坐标;
(2)利用t可表示出OM,则可表示出S,注意分M在y轴右侧和左侧两种情况;
(3)由![]() ,建立关于时间t一元一次方程算出t值,即可得到M点坐标.
,建立关于时间t一元一次方程算出t值,即可得到M点坐标.
解:(1)依题意,令x=0,则有y=6,令y=0,则有x=8,故点A的坐标为(8,0),点B的坐标为(0,6);
(2)依题意,AM=t,
①当点M在y轴右侧时,OM=OA-AM=8-t;![]() (0≤t<8)
(0≤t<8)
②当点M在y轴左侧时,OM=AM-OA=t-8. ![]() (t>8)
(t>8)
(3)∵ON=8,![]() ;
;
![]() ,
,
①当点M在y轴右侧时,![]() ,解得t=5;此时M的坐标为(3,0).
,解得t=5;此时M的坐标为(3,0).
②当点M在y轴左侧时,![]() ,解得t=11,此时M的坐标为(-3,0)
,解得t=11,此时M的坐标为(-3,0)
综上:当t=5或11时,![]() ,此时点M的坐标分别为(3,0),(-3,0).
,此时点M的坐标分别为(3,0),(-3,0).

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目