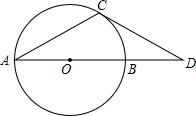
题目内容
如图，△ABC中，以BC上一点O为圆心，以OB为半径的圆交AB于点M，交BC于点N，且BA•BM=BC•BN．
（1）求证：AC⊥BC；
（2）如果CM是⊙O的切线，N为OC的中点，当AC=4时，求AB的值．
（1）求证：AC⊥BC；
（2）如果CM是⊙O的切线，N为OC的中点，当AC=4时，求AB的值．
（1）证明：连接MN，
∵BN是圆的直径，
∴∠BMN=90°，
∵BA•BM=BC•BN，
∴BA：BN=BC：BM，
∴△ACB∽△NMB，
∴∠ACB=∠BMN=90°，
∴AC⊥BC；
（2）连接OM，则∠OMC=90°，
∵N为OC中点，
∴MN=ON=OM，
∴∠MON=60°，
∵OM=OB，
∴∠B=
∠MON=30°，
∵∠ACB=90°，
∴AB=2AC=2×4=8．
∵BN是圆的直径，
∴∠BMN=90°，
∵BA•BM=BC•BN，
∴BA：BN=BC：BM，
∴△ACB∽△NMB，
∴∠ACB=∠BMN=90°，
∴AC⊥BC；
（2）连接OM，则∠OMC=90°，
∵N为OC中点，
∴MN=ON=OM，
∴∠MON=60°，
∵OM=OB，
∴∠B=
| 1 |
| 2 |
∵∠ACB=90°，
∴AB=2AC=2×4=8．
练习册系列答案
阅读快车系列答案
相关题目
交点）．设与AB、l、x轴相切的⊙O1的半径为r1，与AC、l、x轴相切的⊙O2半径为r2
AD1D与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．
