题目内容
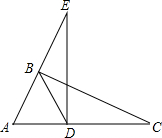 如图,已知点D在AC上,点B在AE上,△ABC≌△ADE,且∠A=∠ABD.若∠A:∠C=5:3,则∠BDE等于( )
如图,已知点D在AC上,点B在AE上,△ABC≌△ADE,且∠A=∠ABD.若∠A:∠C=5:3,则∠BDE等于( )分析:根据全等三角形对应边相等可得AB=AD,根据等角对等边可得AD=BD,从而得到AB=BD=AD,判断出△ABD是等边三角形,根据等边三角形的性质可得∠A=60°,再求出∠C,根据全等三角形对应角相等可得∠E=∠C,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答:解:∵△ABC≌△ADE,
∴AB=AD,
∵∠A=∠ABD,
∴AD=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴∠A=60°,
∵∠A:∠C=5:3,
∴∠C=
×60°=36°,
∵△ABC≌△ADE,
∴∠E=∠C,
在△BDE中,∠BDE=∠ABD-∠E=60°-36°=24°.
故选C.
∴AB=AD,
∵∠A=∠ABD,
∴AD=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴∠A=60°,
∵∠A:∠C=5:3,
∴∠C=
| 3 |
| 5 |
∵△ABC≌△ADE,
∴∠E=∠C,
在△BDE中,∠BDE=∠ABD-∠E=60°-36°=24°.
故选C.
点评:本题考查了全等三角形的性质,等角对等边的性质,等边三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,判断出△ABD是等边三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
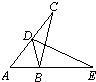 25、如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=5:3,则∠DBC=( )
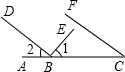
25、如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=5:3,则∠DBC=( )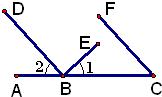 29、如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.
29、如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.