题目内容
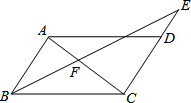 如图,四边形ABCD是平行四边形,点E在CD的延长线上,且CD=2DE,连接BE交AC于点F.
如图,四边形ABCD是平行四边形,点E在CD的延长线上,且CD=2DE,连接BE交AC于点F.(1)求证:△CEF∽△ABF.
(2)若DE=2,AF=2,求AC.
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:(1)由平行四边形的性质可以求得∠1=∠F,又由对顶角的定义得到∠2=∠3,所以根据“两角法”可以证得结论;
(2)由平行四边形的性质得到AB=CD,再结合图中相关线段间的和差关系和(1)中相似三角形的对应边成比例来求线段AC的长度.
(2)由平行四边形的性质得到AB=CD,再结合图中相关线段间的和差关系和(1)中相似三角形的对应边成比例来求线段AC的长度.
解答: (1)证明:如图,∵在?ABCD中,AB∥CD.且点E在CD的延长线上,
(1)证明:如图,∵在?ABCD中,AB∥CD.且点E在CD的延长线上,
∴AD∥CE,
∴∠1=∠F.
又∵∠2=∠3,
∴△CEF∽△ABF;
(2)解:如图,∵CD=2DE,DE=2,
∴CD=4,CE=6.
∴在?ABCD中,AB=CD=4.
又由(1)知:△CEF∽△ABF,
∴
=
,即
=
,
解得FC=3,
则AC=AF+FC=2+3=5,即线段AC的长度是5.
 (1)证明:如图,∵在?ABCD中,AB∥CD.且点E在CD的延长线上,
(1)证明:如图,∵在?ABCD中,AB∥CD.且点E在CD的延长线上,∴AD∥CE,
∴∠1=∠F.
又∵∠2=∠3,
∴△CEF∽△ABF;
(2)解:如图,∵CD=2DE,DE=2,
∴CD=4,CE=6.
∴在?ABCD中,AB=CD=4.
又由(1)知:△CEF∽△ABF,
∴
| FC |
| FA |
| CE |
| AB |
| FC |
| 2 |
| 6 |
| 4 |
解得FC=3,
则AC=AF+FC=2+3=5,即线段AC的长度是5.
点评:本题考查了平行四边形的性质和相似三角形的判定与性质.此题利用了“平行四边形的对边平行且相等”的性质.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
下列说法中不正确的是( )
| A、一个有理数的绝对值一定是正数 |
| B、-5表示的点到原点的距离是5 |
| C、一个有理数的绝对值一定不是负数 |
| D、互为相反数的两个数的绝对值一定相等 |
 如图中有(1)(2)两个直角边长为18等腰直角三角形全等,则图(1)中的小正方形面积是
如图中有(1)(2)两个直角边长为18等腰直角三角形全等,则图(1)中的小正方形面积是 如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、
如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、