题目内容
14.已知反比例函数图象经过点(3,-2),(-1,n),则n等于( )| A. | 5 | B. | -5 | C. | 6 | D. | -6 |
分析 首先设反比例函数关系式为y=$\frac{x}{k}$,根据图象所经过的点可得k=3×(-2)=-n,进而得到函数解析式,再根据反比例函数图象上点的坐标特点可得n的值.
解答 解:设反比例函数关系式为y=$\frac{x}{k}$,(k≠0),则
k=3×(-2)=-n,
解得n=6.
故选:C.
点评 本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
相关题目
5.下列计算中正确的是( )
| A. | a3•a3=a9 | B. | (a3)2=a5 | C. | a2+a3=2a5 | D. | (-a2)3=-a6 |
19.下列图案中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4. 如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )
如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )
 如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )
如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )| A. | -3<x<1 | B. | x>1 | C. | x<-3 | D. | 0<x<1 |
 如图:函数y=ax2+bx+c的图象交x轴于点B,C,交y轴于点A.
如图:函数y=ax2+bx+c的图象交x轴于点B,C,交y轴于点A.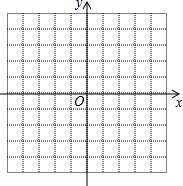 已知一次函数的图象过点A(2,-1)和点B(-1,3),求这个一次函数的表达式并画出它的图象.
已知一次函数的图象过点A(2,-1)和点B(-1,3),求这个一次函数的表达式并画出它的图象. 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM的长为( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM的长为( ) 如图所示,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之积为24,则x+y=18.
如图所示,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之积为24,则x+y=18.