题目内容
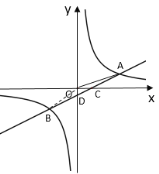
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数的解析式和一次函数的解析式;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)观察图象直接写出![]() 时
时![]() 的取值范围是 ;
的取值范围是 ;
(4)直接写出:![]() 为
为![]() 轴上一动点,当三角形
轴上一动点,当三角形![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标 .
的坐标 .


【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)-2<x<0或x>3;(4)
;(3)-2<x<0或x>3;(4)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)利用待定系数法求出反比例函数的解析式,然后可得点B的坐标,再利用待定系数法求出一次函数的解析式即可;
(2)求出点D的坐标,根据两三角形面积和可得结论;
(3)写出一次函数图象在反比例函数图象上边时对应的x的取值范围即可;
(4)存在三种情况:OA=OP,OA=AP,AP=OP,根据点A的坐标结合图形可得点P的坐标.
解:(1)∵A的坐标是(3,1),
把A的坐标代入![]() 得:k=3,
得:k=3,
即反比例函数的解析式是![]() ,
,
把B(-2,m)代入反比例函数的解析式得:![]() ,
,
即B的坐标是![]() ,
,
把A、B的坐标代入y=ax+b得: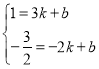 ,
,
解得:![]() ,
,![]() ,
,
即一次函数的解析式是![]() ;
;
(2)连接OB,
在![]() 中,当x=0时,
中,当x=0时,![]() ,即D(0,
,即D(0,![]() ),
),
∴![]() ,
,
∴ △AOB的面积=![]() ;
;
(3)由函数图象得:![]() 时
时![]() 的取值范围是-2<x<0或x>3;
的取值范围是-2<x<0或x>3;
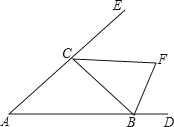
(4)当△AOP是等腰三角形时,存在以下三种情况:
①当OA=OP时,如图2,
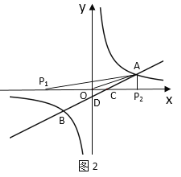
∵A(3,1),
∴OA=![]() ,
,
∴P1(![]() ,0)或P2(
,0)或P2(![]() ,0);
,0);
②当OA=AP时,如图3,
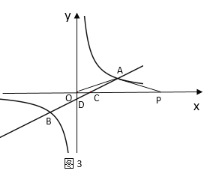
∵A(3,1),
∴P(6,0);
③当OP=AP时,如图4,过A作AE⊥x轴于E,
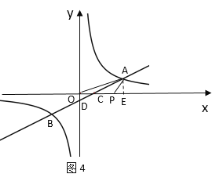
设OP=x,则AP=x,PE=3x,
∴AP2=AE2+PE2,即![]() ,
,
解得:![]() ,
,
∴P(![]() ,0);
,0);
综上,P的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

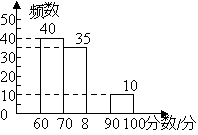
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如下:
频率分布统计表 | 频率分布直方图 | ||
分数段 | 频数 | 频率 |
|
60≤x<70 | 40 | 0.40 | |
70≤x<80 | 35 | b | |
80≤x<90 | a | 0.15 | |
90≤x<100 | 10 | 0.10 | |
请根据上述信息,解答下列问题:
(1)表中:a= ,b= ;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数。