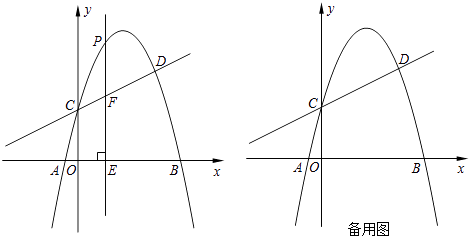题目内容
【题目】在平面直角坐标系中,直线![]() :
:![]() 分别与x轴、y轴交于点A、点B,且与直线
分别与x轴、y轴交于点A、点B,且与直线![]() :
:![]() 于点C.
于点C.
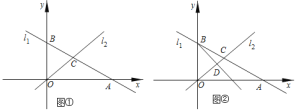
![]() Ⅰ
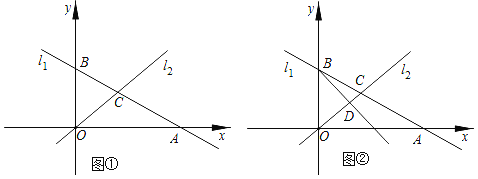
Ⅰ![]() 如图
如图![]() ,求出B、C两点的坐标;
,求出B、C两点的坐标;
![]() Ⅱ
Ⅱ![]() 若D是线段OC上的点,且
若D是线段OC上的点,且![]() 的面积为4,求直线BD的函数解析式.
的面积为4,求直线BD的函数解析式.
![]() Ⅲ
Ⅲ![]() 如图
如图![]() ,在
,在![]() Ⅱ
Ⅱ![]() 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(Ⅰ)B(0,4)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ) Q的坐标为(2√2,-2√2)或(-2,2)或(4,4).
;(Ⅲ) Q的坐标为(2√2,-2√2)或(-2,2)或(4,4).
【解析】
(1) 令![]() ,得到
,得到![]() ,可求B坐标,解方程组可得得解得C的坐标;(2)由面积求出D的坐标,再由待定系数法求BD函数解析式;(3)
,可求B坐标,解方程组可得得解得C的坐标;(2)由面积求出D的坐标,再由待定系数法求BD函数解析式;(3)![]() 当OB为菱形的边时,
当OB为菱形的边时,![]() ,可得
,可得![]() ,
,![]() 当
当![]() 为菱形的对角线时,四边形
为菱形的对角线时,四边形![]() 是正方形,此时
是正方形,此时![]() .
.![]() 当OB为菱形的边时,点
当OB为菱形的边时,点![]() 与D重合,P、Q关于y轴对称,
与D重合,P、Q关于y轴对称,![]() .
.
解:![]() Ⅰ
Ⅰ![]() 对于直线:
对于直线:![]() ,令
,令![]() ,得到
,得到![]() ,
,![]() ,
,
由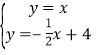 ,解得
,解得![]() ,
,
![]()
![]() Ⅱ
Ⅱ![]() 点D在直线
点D在直线![]() 上,设
上,设![]() ,
,![]() 的面积为4,
的面积为4,![]() ,
,
解得![]() ,
,![]() .
.
设直线BD的解析式为![]() ,则有
,则有![]() ,
,
解得![]() ,
,![]() 直线BD的解析式为
直线BD的解析式为![]() .
.![]() Ⅲ
Ⅲ![]() 如图
如图![]() 中,
中,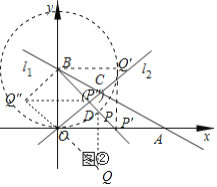
![]() 当OB为菱形的边时,
当OB为菱形的边时,![]() ,可得
,可得![]() ,
,![]()
![]() 当
当![]() 为菱形的对角线时,四边形
为菱形的对角线时,四边形![]() 是正方形,此时
是正方形,此时![]() .
.![]() 当OB为菱形的边时,点
当OB为菱形的边时,点![]() 与D重合,P、Q关于y轴对称,
与D重合,P、Q关于y轴对称,![]() ,
,
综上所述,满足条件的Q的坐标为![]() 或
或![]() 或
或![]() .
.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案【题目】从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解”雾霾天气的主要原因“,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: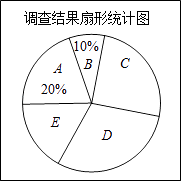
(1)填空:m= , n= . 扇形统计图中E组所占的百分比为%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?