题目内容
【题目】点A在数轴上对应的数为a,点B对应的数为b,且a,b满足:|a+3|+(b-2)2=0
(1)求线段AB的长;
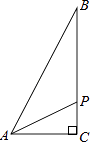
(2)如图①,点C在数轴上对应的数为x,且是方程![]() 的根,在数轴上是否存在点M使MA+MB=
的根,在数轴上是否存在点M使MA+MB=![]() BC+AB?若存在,求出点M对应的数;若不存在,说明理由;
BC+AB?若存在,求出点M对应的数;若不存在,说明理由;
(3)如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断![]() 的值是不变的还是变的,如果不变请直接写出其值,如果是变的请说明理由.
的值是不变的还是变的,如果不变请直接写出其值,如果是变的请说明理由.
【答案】(1)线段AB的长为5;(2)存在,当点M表示的数为﹣5或4时,MA+MB=![]() BC+AB;(3)
BC+AB;(3)![]() 的值不变,为
的值不变,为![]() .
.
【解析】
(1)利用非负数的性质求出a与b的值,即可确定出AB的长;
(2)求出已知方程的解确定出x,得到C表示的点,设点M在数轴上对应的数是m,由MA+MB=![]() BC+AB确定出M位置,即可做出判断;
BC+AB确定出M位置,即可做出判断;
(3)设N点所表示的数为n,就有NA=n+3,NB=n﹣2,根据条件就可以表示出NQ=![]() NA=
NA=![]() ,BP=
,BP=![]() NB=
NB=![]() (n﹣2),再代入
(n﹣2),再代入![]() 求出其值即可.
求出其值即可.
(1)∵|a+3|+(b﹣2)2=0,
∴a+3=0,b﹣2=0,
∴a=﹣3,b=2,
∴AB=|﹣3﹣2|=5.
答:线段AB的长为5;
(2)存在,
∵x+1=![]() x﹣2,
x﹣2,
∴x=﹣6,
∴BC=8.
设点M在数轴上对应的数是m,
∵MA+MB=![]() BC+AB,
BC+AB,
∴|m+3|+|m﹣2|=![]() ×8+5,
×8+5,
令m+3=0,m﹣2=0,
∴m=﹣3或m=2.
①当m≤﹣3时,
﹣m﹣3+2﹣m=9, m=﹣5;
②当﹣3<m≤2时,
m+3+2﹣m=9(舍去);
③当m>2时,
m+3+m﹣2=9,
m=4.
∴当点M表示的数为﹣5或4时,MA+MB=![]() BC+AB;
BC+AB;
(3)设N点所表示的数为n,
∴NA=n+3,NB=n﹣2.
∵NA的中点为Q,
∴NQ=![]() NA=
NA=![]() ,
,
P为NB的三等分点且靠近于B点,
∴BP=![]() NB=
NB=![]() (n﹣2),
(n﹣2),
∴![]() ×
×![]() -
-![]() ×
×![]() (n-2)=
(n-2)=![]() ,
,
故![]() 的值是不变的.
的值是不变的.

 阅读快车系列答案
阅读快车系列答案