Question

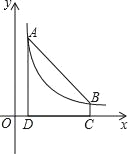
【题目】如图1，已知平面直角坐标系中，点，满足．

（1）求的面积；

（2）将线段经过水平、竖直方向平移后得到线段，已知直线经过点的横坐标为5．

①求线段平移过程中扫过的面积；

②请说明线段的平移方式，并说明理由；

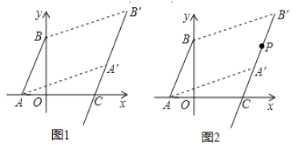
③如图2，线段上一点，直接写出之间的数量关系．

Answer 1

【答案】（1）；（2）①平行四边形；②线段先向右平移7个单位，再向上平移2个单位得到线段，③．

【解析】

（1）利用非负数的性质求出a、b的值即可解决问题；

（2）①根据平移的性质得平行四边形与三角形等底等高，再根据三角形面积公式求解即可；

②过作x轴于，过作轴于，垂足分别为，根据题意可设，由三角形梯形平行四边形三角形三角形可列方程解出b值，从而可得结果；

③利用待定系数法求出A′B′的表达式即可解决问题．

（1），.

且

当时，

，

三角形

（2）①由平移性质可知，，

点到的距离=点到的距离

故平行四边形与三角形等底等高

平行四边形三角形

又三角形中，，高

三角形

平行四边形

②过作x轴于，过作轴于，垂足分别为

由的横坐标为5，的横坐标为可知，线段平移规律是先向右移动了7个单位，

不妨设

三角形梯形平行四边形三角形三角形

即，

解得：b=2，

由上可知，（5，2），故线段先向右平移7个单位，再向上平移2个单位得到线段.

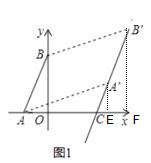
③ ，

∵在线段上，（5，2），B′（7，6），

设直线A′B′的表达式为y=px+q，将A′和B′代入，

得，

解得：，

∴直线A′B′的表达式为y=2x-8，

∴m和n的关系式为：.