题目内容
 如图,AB与CD相交于点O,∠D=∠B=90°,要使△AOD与△COB全等,还需要添加一个条件,你认为添加的条件可以是
如图,AB与CD相交于点O,∠D=∠B=90°,要使△AOD与△COB全等,还需要添加一个条件,你认为添加的条件可以是考点:全等三角形的判定
专题:开放型
分析:要使△AOD≌△COB,已知AB与CD相交于点O,∠D=∠B=90°,具备了两角对应相等,还缺少边对应相等的条件,结合判定方法及图形进行选择即可.
解答:解:DO=BO,
理由是:∵AB与CD相交于点O,
∴∠AOD=∠COB
∵在△AOD和△COB中
∴△AOD≌△COB,
故答案为:DO=BO.
理由是:∵AB与CD相交于点O,
∴∠AOD=∠COB
∵在△AOD和△COB中
|
∴△AOD≌△COB,
故答案为:DO=BO.
点评:本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,此题答案不唯一,如:DO=BO或AD=CB或AO=CO.

练习册系列答案
相关题目
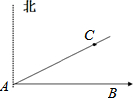 如图,测得A点到灯塔C点的距离为10海里,灯塔C点在A点东偏北30°方向上,一轮船由A点出发向正东方向航行,当此轮船行至距A点
如图,测得A点到灯塔C点的距离为10海里,灯塔C点在A点东偏北30°方向上,一轮船由A点出发向正东方向航行,当此轮船行至距A点 如图,五角星ABCDE中,∠AMB=
如图,五角星ABCDE中,∠AMB=