题目内容
阅读下面的材料:∵ax2+bx+c=0(a≠0)的根为x1=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
∴x1+x2=
| -2b |
| 2a |
| b |
| a |
| b2-(b2-4ac) |
| 4a2 |
| c |
| a |
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
| b |
| a |
| c |
| a |
请利用这一结论解决下列问题:
(1)若x2-px+q=0的两根为-1和3,求p和q的值;
(2)设方程3x2+2x-1=0的根为x1、x2,求
| 1 |
| x1 |
| 1 |
| x2 |
分析:(1)直接根据根与系数的关系解题.
(2)先将代数式变形
+
=
,再利用根与系数的关系解题.
(2)先将代数式变形
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
解答:解:(1)∵x2-px+q=0的两根为x1=-1,x2=3.
由结论可知x1+x2=p,x1•x2=q.
∴p=-1+3=2,q=-1×3=-3.
(2)∵3x2+2x-1=0的两根为x1、x2.
∴x1+x2=-
,x1•x2=-
.
∴
+
=
=
=2.
由结论可知x1+x2=p,x1•x2=q.
∴p=-1+3=2,q=-1×3=-3.
(2)∵3x2+2x-1=0的两根为x1、x2.
∴x1+x2=-
| 2 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
-
| ||
-
|
点评:此题是一道材料分析题,详尽的说明了各根与系数以及两个根的和、积与系数的关系.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
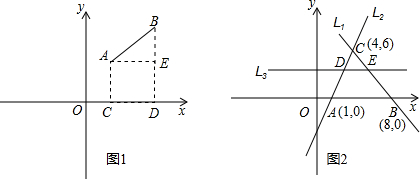
 (2013•湛江)阅读下面的材料,先完成阅读填空,再按要求答题:
(2013•湛江)阅读下面的材料,先完成阅读填空,再按要求答题: