题目内容
已知实数a、b满足条件a2+b2+a2b2=4ab-1,则
- A.
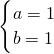
- B.
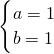 或
或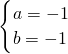
- C.
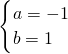 或
或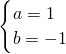
- D.
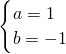
B
分析:把右边的两项移到左边,再把4ab分成2ab+2ab,然后分别与左边的四项组成两个完全平方形式,从而出现两个非负数的和等于0的形式,那么每一个非负数都等于0,解关于a、b的方程,从而求出a、b的值.
解答:∵a2+b2+a2b2=4ab-1,
∴a2-2ab+b2+a2b2-2ab+1=0,
∴(a-b)2+(ab-1)2=0,
∴a-b=0,ab-1=0,
解得a=1,b=1或a=b=-1,
故选B.
点评:本题主要考查完全平方公式.完全平方公式:(a±b)2=a2±2ab+b2.注意会正确的拆项.
分析:把右边的两项移到左边,再把4ab分成2ab+2ab,然后分别与左边的四项组成两个完全平方形式,从而出现两个非负数的和等于0的形式,那么每一个非负数都等于0,解关于a、b的方程,从而求出a、b的值.
解答:∵a2+b2+a2b2=4ab-1,
∴a2-2ab+b2+a2b2-2ab+1=0,
∴(a-b)2+(ab-1)2=0,
∴a-b=0,ab-1=0,
解得a=1,b=1或a=b=-1,
故选B.
点评:本题主要考查完全平方公式.完全平方公式:(a±b)2=a2±2ab+b2.注意会正确的拆项.

练习册系列答案
相关题目
 ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由. ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由. ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.