题目内容
4.通常用[x]来表示不大于x的整数,如[1]=1,[0.5]=0,[-1.5]=-2,那么[$\frac{2}{3}$+$\frac{1}{2012}$]+[$\frac{2}{3}$+$\frac{2}{2012}$]+…+[$\frac{2}{3}$+$\frac{2010}{2012}$]+[$\frac{2}{3}$+$\frac{2011}{2012}$]的值为( )| A. | 1340 | B. | 1341 | C. | 669 | D. | 670 |
分析 本题[$\frac{2}{3}$+$\frac{1}{2012}$]=0,[$\frac{2}{3}$+$\frac{2}{2012}$]=0,…,[$\frac{2}{3}$+$\frac{670}{2012}$]=0,[$\frac{2}{3}$+,$\frac{671}{2012}$]=1,[$\frac{2}{3}$+$\frac{672}{2012}$]=1,…,[$\frac{2}{3}$+$\frac{2011}{2012}$]=1,再相加即可求解.
解答 解:∵[1]=1,[0.5]=0,[-1.5]=-2,
∴[$\frac{2}{3}$+$\frac{1}{2012}$]=0,[$\frac{2}{3}$+$\frac{2}{2012}$]=0,…,[$\frac{2}{3}$+$\frac{670}{2012}$]=0,[$\frac{2}{3}$+,$\frac{671}{2012}$]=1,[$\frac{2}{3}$+$\frac{672}{2012}$]=1,…,[$\frac{2}{3}$+$\frac{2011}{2012}$]=1,
∴[$\frac{2}{3}$+$\frac{1}{2012}$]+[$\frac{2}{3}$+$\frac{2}{2012}$]+…+[$\frac{2}{3}$+$\frac{2010}{2012}$]+[$\frac{2}{3}$+$\frac{2011}{2012}$]
=0×670+1×(2011-671+1)
=0+1×1341
=0+1341
=1341.
故选:B.
点评 本题考查了取整函数的知识,难度较大,属于规律性题目,解答本题的关键是将{}按组别去掉,这样可得出规律,一定要注意有特殊到一般的总结,如果不能立即发现规律应多计算前面的几组,计算的多了,规律自然就容易发现.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | 等边三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
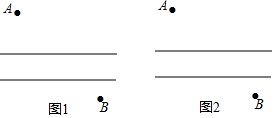 如图,单位A与B分别位于一条封闭式街道的两旁,现在准备合作修建一条过街天桥(桥必须与街道垂直),问:
如图,单位A与B分别位于一条封闭式街道的两旁,现在准备合作修建一条过街天桥(桥必须与街道垂直),问: