题目内容
直线y=x-2与坐标轴交于A、B两点，点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C最多有________个．
7
分析：首先画出直线与x、y轴的交点，△ABC为等腰三角形，分别设AB=AC，AB=BC，AC，AC=BC．三种情况，找出符合条件的C点．
解答：
解：如图所示：
以C为顶点，CB=CA，则C点坐标（0，0）；
以B为顶点，BC=BA，则C点坐标（-2，0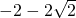），（0，
），（0，
）；
以A为顶点，AB=AC，则C点坐标（0，2），（
，0），（
，0）．
共有7个坐标，所以满足条件的点C最多有7个．
点评：本题主要考查对一次函数的认识和思考问题的全面性，要注意要分别以三角形三个点做顶点，找出全部的满足条件的C点．
分析：首先画出直线与x、y轴的交点，△ABC为等腰三角形，分别设AB=AC，AB=BC，AC，AC=BC．三种情况，找出符合条件的C点．
解答：
解：如图所示：以C为顶点，CB=CA，则C点坐标（0，0）；
以B为顶点，BC=BA，则C点坐标（-2，0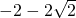），（0，
），（0，）；以A为顶点，AB=AC，则C点坐标（0，2），（
，0），（，0）．共有7个坐标，所以满足条件的点C最多有7个．
点评：本题主要考查对一次函数的认识和思考问题的全面性，要注意要分别以三角形三个点做顶点，找出全部的满足条件的C点．
练习册系列答案
相关题目
C、D，且C点的坐标为（-1，2）．在直角坐标系中，若一点的纵横坐标都是整数，则称该点为整点．设k为整数，当直线y=x-2与y=kx+k的交点为整点时，k的值可以取（ ）
| A、4个 | B、5个 | C、6个 | D、7个 |
等腰梯形ABCD（AB＞CD），且等腰梯形的面积是8
如图，已知直线y=x+2与y轴交于点A，与抛物线y=-x2+3x+5交于B，C两点．