题目内容
15. 如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度;(结果保留两位小数)
如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度;(结果保留两位小数)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
分析 过点M的水平线交直线AB于点H,设MH=x,则AH=x,结合等腰直角三角形的性质和解直角三角形ABH得到AB=AH-BH=x-0.60x=0.4x=3.5,由此求得MH的长度,则MN=AB+BH.
解答 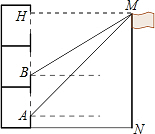 解:过点M的水平线交直线AB于点H,
解:过点M的水平线交直线AB于点H,
由题意,得∠AMH=∠MAH=45°,∠BMH=31°,AB=3.5,
设MH=x,则AH=x,BH=xtan31°=0.60x,
∴AB=AH-BH=x-0.60x=0.4x=3.5,
解得x=8.75,
则旗杆高度MN=x+1=9.75(米)
答:旗杆MN的高度度约为9.75米.
点评 本题考查了解直角三角形--仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
6.已知$\frac{a}{b}$=$\frac{2}{3}$,那么$\frac{a}{a+b}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
3.P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.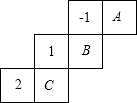 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )| A. | -1,-2,1 | B. | -1,1,-2 | C. | -2,-1,1 | D. | 1,-1,-2 |
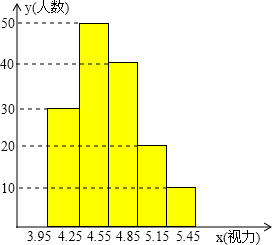 当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的条形图(长方形的高表示该组人数)如下:
当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的条形图(长方形的高表示该组人数)如下: 如图所示,长方形的长为a,宽为b,写出计算阴影部分的面积S的公式;当a=3,b=2时,求S的值.
如图所示,长方形的长为a,宽为b,写出计算阴影部分的面积S的公式;当a=3,b=2时,求S的值.