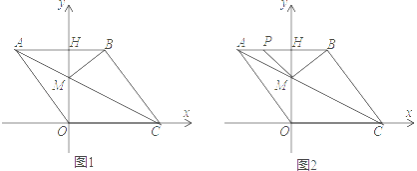题目内容
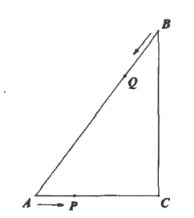
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)求出点Q的从B到A的运动时间,再求出AP的长,利用勾股定理即可解决问题.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.根据DQ=CK,构建方程即可解决问题.
(3)分两种情形:如图3-1中,当∠APQ=90°时,如图3-2中,当∠AQP=90°时,分别构建方程即可解决问题.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
点Q运动到点A时,t=![]() =5,
=5,
∴AP=5,PC=1,
在Rt△PBC中,PB=![]() .
.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
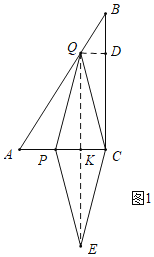
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴![]() ,
,
解得t=![]() .
.
∴t=![]() s时,四边形PQCE是菱形.
s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
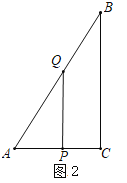
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3中,当∠AQP=90°时,
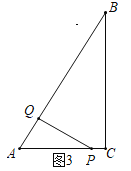
∵△AQP∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() s时,△APQ是直角三角形.
s时,△APQ是直角三角形.

【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
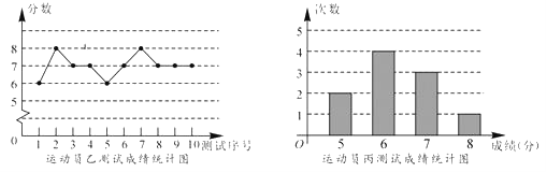
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)