题目内容
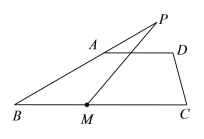
【题目】已知：AD∥BC，点P为直线AB上一动点，点M在线段BC上，连接MP，
，
，
．
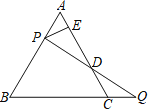
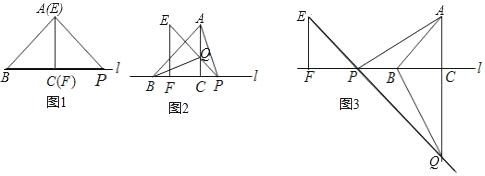
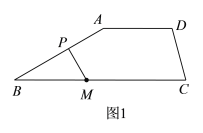
（1）如图1，当点P在线段AB上时，若
，
=150°，则
=________°；
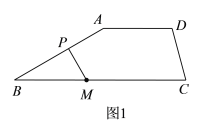
（2）如图2，当点P在AB的延长线上时，写出，
与之间的数量关系，并说明理由；
（3）如图3，当点P在BA的延长线上时，请画出图形，直接写出，与之间的数量关系．
【答案】（1）120°；（2） 
，证明见解析；（3）图见解析，
【解析】
（1）根据两直线平行，同旁内角互补求出∠B，然后利用三角形的外角的性质求出γ.
（2）过点N作
∥
，根据两直线平行，内错角相等，因为∥
，所以
∥，两条直线平行内错角相等，即可得解.
（3）根据两直线平行，同旁内角互补求出∠B，然后然后利用三角形的外角的性质求列式计算即可得解．
（1）∵AD∥BC，
=150°
∴
∴
∵MP⊥AB
∴∠APM=
∴
故答案：
（2）
证明：如图所示，
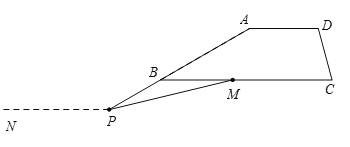
过点
作∥
∴
∵∥
∴∥
∴
∴
即：
故答案：
（3）∵AD∥BC
∴
∵∠PMC=∠B+∠APM
∴
故答案：
练习册系列答案
名校课堂系列答案
相关题目
