Question

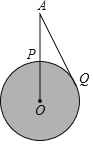
【题目】如图，某航天飞机在地球表面点P的正上方A处，从A处观测到地球上的最远点Q，即AQ是⊙O的切线，若∠QAP＝α，地球半径为R，

求：(1)航天飞机距地球表面的最近距离AP的长；

(2)P、Q两点间的地面距离，即的长．(注：本题最后结果均用含α，R的代数式表示)

Answer 1

【答案】（1）AP＝﹣R；（2）

【解析】

(1)连接OQ，根据题意可得：AQ是⊙O的切线，然后由切线的性质，可得OQ⊥AQ，又由∠QAP＝α，地球半径为R，即可求得OA的长，继而求得航天飞船距离地球表面的最近距离AP的值；

(2)在直角△OAQ中，可求出∠O的度数，再利用弧长公式计算即可．

解：

(1)由题意，从A处观测到地球上的最远点Q，

∴AQ是⊙O的切线，切点为Q，

连接OQ，则OQ垂直于AQ，如图，

则在直角△OAQ中有＝sinα，

即AP＝﹣R；

(2)在直角△OAQ中，

则∠O＝90°﹣α，

由弧长公式得的长＝．