Question

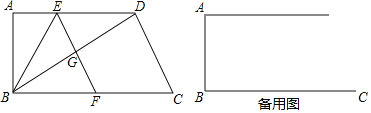
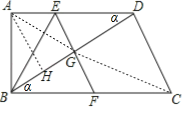
【题目】如图，在四边形ABCD中AD∥BC，∠A＝90°，AB＝6，BC＝10，点E为边AD上一点，将ABE沿BE翻折，点A落在对角线BD上的点G处，连接EG并延长交射线BC于点F．

（1）如果cos∠DBC，求EF的长；

（2）当点F在边BC上时，连接AG，设AD＝x，y，求y关于x的函数关系式并写出x的取值范围；

（3）连接CG，如果△FCG是等腰三角形，求AD的长．

Answer 1

【答案】（1）EF＝9；（2）y（x）；（3）AD的长为或

【解析】

（1）利用S△BEF=BFAB=EFBG，即可求解；

（2）过点A作AH⊥BG交于点H，连接AG，设：BF＝a，先表示出AH，根据三角形面积公式可得y，由tanα可得a2＝36+（）2，整理可得y关于x的函数关系式，根据BF≤10可求出x的取值范围.

（3）分GF=FC、CF=CG两种情况，求解即可．

（1）将△ABE沿BE翻折，点A落在对角线BD上的点G处，

∴BG⊥EF，BG＝AB＝6，

cos∠DBC，则：BF＝9，

S△BEFBFABEFBG，即：9×6＝6×EF，

则EF＝9；

（2）过点A作AH⊥BG交于点H，连接AG，设：BF＝a，

在Rt△BGF中， cosα，则tanα，

∵∠BAH+∠ABH=90°，∠ADB+∠ABH=90°，

∴∠BAH=∠ADB= a，

∴AH=6cos a，

∴y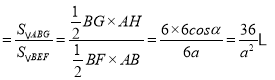①，

∵tanα，

∴a2＝36+（）2…②，

把②式代入①式整理得：y；

∵BF≤10，

∴36+（）2≤100，

解之得x，

∴y（x）；

（3）①当GF＝FC时，

∵cosα，

∴，

∴BF=，

∴FC=10-，

∵sinα=，

∴，

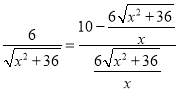整理得,

4x2-45x=0，

∴x1，x2=0（舍去），

∴AD；

②当CF＝CG时，

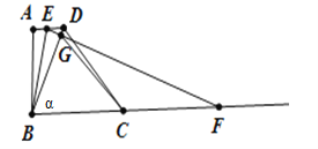
∵CF＝CG，

∴∠CFG=∠CGF，

∵∠CFG+∠CBG=90°，∠CGF+∠CGB=90°，

∴∠CBG=∠CGB，

∴CG=CB=CF=10，

∴BF=20.

∵sinα=，

∴，

整理得

91x2=324，

∴x1，x2（舍去）；

故：AD的长为或．