题目内容
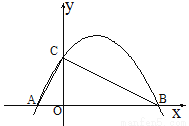
如图,在平面直角坐标系中,抛物线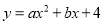 与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
练习册系列答案
相关题目
题目内容
如图,在平面直角坐标系中,抛物线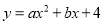 与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
