题目内容
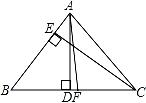
如图,在△ABC中,AD,CE是高线,AF是角平分线,∠BAC=∠AFD=80°.
(1)求∠BCE的度数;
(2)如果AD=6,BE=5.求△ABC的面积.
【考点】三角形内角和定理;三角形的面积;含30度角的直 角三角形.
角三角形.
【分析】(1)先由直角三角形的性质求出∠ADF的度数,再由角平分线的性质求出∠BAF的度数,故可得出∠BAD的度数,再由直角三角形的性质即可得出结论;
(2)由(1)知,∠BCE=30°,故可得出BC=2BE,再由三角形的面积公式即可得出结论.
【解答】解:(1 )∵AD,CE是高线,
)∵AD,CE是高线,
∴∠BEC=∠ADB=∠ADC=90°.
∴∠DAF=90°﹣∠AFD=90°﹣80°=10°.
∵AF平分∠BAC,
∴∠BAF= ∠BAC=
∠BAC= ×80°=40°.
×80°=40°.
∴∠BAD=∠BAF﹣∠DAF=40°﹣10°=30°.
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BCE=∠BAD=30°.

(2)在Rt△BCE中,
∵∠BCE=30°,
∴BC=2BE=2×5=10.
∴S△ABC= BC•AD=
BC•AD= ×10×6=30.
×10×6=30.
【点评】本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目

 =
=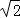 ﹣1,
﹣1, =
= ,
, =2﹣
=2﹣ …请利用你发现的规律计算:
…请利用你发现的规律计算: +…+
+…+ )×(
)×( +
+ )=__________.
)=__________. ,下列分式中与其相等的是( )
,下列分式中与其相等的是( ) B.
B. C.
C. D.
D.
 ;
;
 B.
B.
 C.
C.
 D.
D.

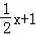
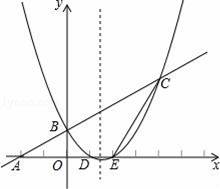
 的图象与x轴交于A点,与y轴交于B点:抛物线y=
的图象与x轴交于A点,与y轴交于B点:抛物线y=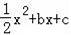
 的图象余一次函数y=
的图象余一次函数y=