题目内容
两圆内切,圆心距为1,一圆半径为3,则另一圆半径是
- A.2
- B.4
- C.2或4
- D.无法确定
C
分析:由内切两圆的圆心距为1,分别从若大圆的半径为3与若小圆的半径为3去分析,然后根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可求得另一圆的半径.
解答:设另一圆的半径为r,
∵两圆内切,
∴1=3-r或1=r-3,则r=2或4,
∴两圆内切,另一圆的半径为2或4.
故选C.
点评:本题考查了圆与圆的位置关系,用到的知识点为:两圆外切,圆心距=两圆半径之和.两圆内切,圆心距=两圆半径之差.
分析:由内切两圆的圆心距为1,分别从若大圆的半径为3与若小圆的半径为3去分析,然后根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可求得另一圆的半径.
解答:设另一圆的半径为r,
∵两圆内切,
∴1=3-r或1=r-3,则r=2或4,
∴两圆内切,另一圆的半径为2或4.
故选C.
点评:本题考查了圆与圆的位置关系,用到的知识点为:两圆外切,圆心距=两圆半径之和.两圆内切,圆心距=两圆半径之差.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
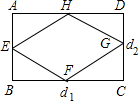 已知⊙O1和⊙O2的半径分别是8.5cm和3.5cm,当两圆外切时圆心距为d1,两圆内切时圆心距为d2,如图,以d1和d2长为邻边作矩形ABCD,依次连接矩形ABCD四边中点,得四边形EFGH,则四边形EFGH周长是
已知⊙O1和⊙O2的半径分别是8.5cm和3.5cm,当两圆外切时圆心距为d1,两圆内切时圆心距为d2,如图,以d1和d2长为邻边作矩形ABCD,依次连接矩形ABCD四边中点,得四边形EFGH,则四边形EFGH周长是